
【题目】如图,OA⊥OB,引射线OC(点C在∠AOB外),若∠BOC=α(0°<α<90°),OD平分∠BOC,OE平分∠AOD.
(1)若α=40°,求∠BOE的度数;
(2)请根据∠BOC=α,请依题意补全图形,求出∠BOE的度数(用含α的式子表示).

【答案】(1)35°;(2)45°-![]() α.
α.
【解析】
(1)根据角平分线的定义可得∠COD=∠BOD=20°, 继而可得∠AOD的度数,进而由OE是∠AOD的平分线求得∠DOE的度数即可求得答案;
(2)先根据题意补全图形,然后根据角平分线的定义可得∠COD=∠BOD=![]() α,继而可得∠AOD=
α,继而可得∠AOD=![]() α+90°,再由OE是∠AOD的平分线,可得∠DOE=
α+90°,再由OE是∠AOD的平分线,可得∠DOE=![]() α+45°,进而根据∠BOE=∠DOE﹣∠BOD即可求得答案.
α+45°,进而根据∠BOE=∠DOE﹣∠BOD即可求得答案.
(1)∵OA⊥OB,
∴∠AOB=90°,
∵OD是∠BOC的平分线,
∴∠COD=∠BOD=![]() ∠BOC=
∠BOC=![]() ×40°=20°,
×40°=20°,
∴∠AOD=∠BOD+∠AOB=20°+90°=110°,
又∵OE是∠AOD的平分线,
∴∠DOE=![]() ∠AOD=55°,
∠AOD=55°,
∴∠BOE=∠DOE﹣∠BOD=55°-20°=35°;
(2)补全图形如下:
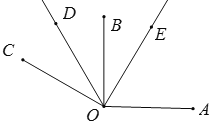
∵OA⊥OB,
∴∠AOB=90°,
∵OD是∠BOC的平分线,
∴∠COD=∠BOD=![]() ∠BOC=
∠BOC=![]() α,
α,
∴∠AOD=∠BOD+∠AOB=![]() α+90°,
α+90°,
又∵OE是∠AOD的平分线,
∴∠DOE=![]() ∠AOD=
∠AOD=![]() (
(![]() α+90°)=
α+90°)=![]() α+45°,
α+45°,
∴∠BOE=∠DOE﹣∠BOD=![]() α+45°-
α+45°-![]() α=45°-
α=45°-![]() α.
α.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
【题目】观察下列各式
(x﹣1)(x+1)=x2﹣1
(x﹣1)(x2+x+1)=x3﹣1
(x﹣1)(x3+x2+x+1)=x4﹣1
(1)根据以上规律,则(x﹣1)(x6+x5+x4+x3+x2+x+1)= ;
(2)你能否由此归纳出一般规律(x﹣1)(xn+xn﹣1+……+x+1)= ;
(3)根据以上规律求32018+32017+32016+…32+3+1的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上A 点对应的数为﹣5,B 点在A 点右边,电子蚂蚁甲、乙在B分别以2个单位/秒、1个单位/秒的速度向左运动,电子蚂蚁丙在A 以3个单位/秒的速度向右运动.
(1)若电子蚂蚁丙经过5秒运动到C 点,求C 点表示的数;
![]()
(2)若它们同时出发,若丙在遇到甲后1秒遇到乙,求B 点表示的数;
![]()
(3)在(2)的条件下,设它们同时出发的时间为t 秒,是否存在t的值,使丙到乙的距离是丙到甲的距离的2倍?若存在,求出t 值;若不存在,说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:关于x的二次函数![]() 的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使△PBC为等腰三角形.若存在,请求出点P的坐标;
(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到 达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新个税法于2018年9月1日全面实施,工资、薪金所得基本减除费用标准由3500元提高至5000元,并按新的税率表计算纳税:
序号 | 税前每月工资的各部分 | 税率 |
1 | 不超过5000元部分 | 0% |
2 | 超过5000元至8000元的部分 | 3% |
3 | 超过8000元至17000元的部分 | 10% |
4 | 超过17000元至30000元的部分 | 20% |
5 | 超过30000元至40000元的部分 | 25% |
6 | 超过40000元至60000元的部分 | 30% |
7 | 超过60000元至80000元的部分 | 35% |
8 | 超过80000元的部分 | 45% |
(1)在新个税法实施后,小王没扣税前某月工资7800元,他这个月应交税 元;
(2)在新个税法实施后,若小李没扣税前某月工资x元![]() ,他这个月交税y元,则y= ;
,他这个月交税y元,则y= ;
(3)在新个税法实施后,一企业某月把奖金放在工资里发放(奖金跟工资一起扣税),该企业员工小刘这个月领取了工资加奖金(税后)26410元.已知小刘没扣税前工资为a元![]() ,若工资和奖金分两次发放(工资扣税,奖金不扣税),小刘这个月可以领取多少钱?(如需要,可用含a 的代数式表示)
,若工资和奖金分两次发放(工资扣税,奖金不扣税),小刘这个月可以领取多少钱?(如需要,可用含a 的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下表三行数的规律,回答下列问题:
第1列 | 第2列 | 第3列 | 第4列 | 第5列 | 第6列 | … | |
第1行 | -2 | 4 | -8 | a | -32 | 64 | … |
第2行 | 0 | 6 | -6 | 18 | -30 | 66 | … |
第3行 | -1 | 2 | -4 | 8 | -16 | b | … |
(1)第1行的第四个数a是 ;第3行的第六个数b是 ;
(2)若第1行的某一列的数为c,则第2行与它同一列的数为 ;
(3)已知第n列的三个数的和为2562,若设第1行第n列的数为x,试求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“PM2.5”指数是空气中可入肺颗粒物的含量,是空气质量的指标之一.下表为A市1﹣12月“PM2.5月平均指数”(单位:微克/立方米)
PM2.5指数 | 20 | 30 | 40 | 41 | 43 | 50 |
月数 | 2 | 4 | 3 | 1 | 1 | 1 |
(1)求这12个月“PM2.5月平均指数”的众数、中位数、平均数;
(2)根据《环境空气质量标准》,宜居城市的标准之一是“PM2.5年平均指数少于35微克/立方米”,请你判断A市是否为宜居城市?
查看答案和解析>>
科目:初中数学 来源: 题型:
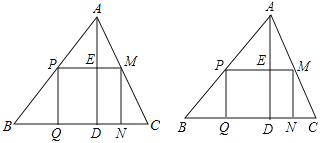
【题目】如图:有一块余料的形状是锐角三角形ABC,边BC=120mm,高AD=80mm.
(1)如果把它加工成长方形零件,使长方形的一边在BC上,其余两个顶点分别在AB、AC上,设长方形宽xmm,面积为ymm2,那么宽为多少时,其面积最大.最大面积是多少?
(2)若以BC的中点O为原点建立平面直角坐标系,B(-60,0),AD=BD.
求过A、B、C三点的抛物线解析式;
在此抛物线对称轴上是否存在一点R,使以A、B、R为顶点的三角形是直角三角形.若存在,请直接写出R点的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学中,运用整体思想方法在求代数式的值中非常重要.
例如:已知:a2+2a=1,则代数式2a2+4a+4=2( a2+2a) +4=2×1+4=6.
请你根据以上材料解答以下问题:
(1)若![]() ,求
,求![]() 的值;
的值;
(2)当![]() 时,代数式
时,代数式![]() 的值是5,求当
的值是5,求当![]() 时,代数式px3+qx+1的值;
时,代数式px3+qx+1的值;
(3)当![]() 时,代数式
时,代数式![]() 的值为m,求当
的值为m,求当![]() 时,求代数式
时,求代数式![]() 的值是多少?
的值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com