
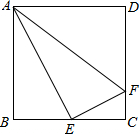
 如图,在正方形ABCD中,点E为BC的中点,CF=$\frac{1}{4}$CD,连接AE、AF、EF.设CF=a
如图,在正方形ABCD中,点E为BC的中点,CF=$\frac{1}{4}$CD,连接AE、AF、EF.设CF=a分析 (1)由正方形的性质得出AB=BC=CD=DA,∠B=∠C=∠D=90°,由已知条件得出AD=DA=4a,BE=CE=2a,DF=3a,由勾股定理求出AE、AF、EF即可;
(2)求出AE2+EF2=AF2,根据勾股定理的逆定理即可得出结论.
解答 (1)解:∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠B=∠C=∠D=90°,
∵点E为BC的中点,CF=$\frac{1}{4}$CD,CF=a,
∴AD=DA=4a,BE=CE=2a,DF=3a,
∴AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=$\sqrt{(4a)^{2}+(2a)^{2}}$=2$\sqrt{5}$a,
AF=$\sqrt{D{A}^{2}+D{F}^{2}}$=$\sqrt{(4a)^{2}+(3a)^{2}}$=5a,
EF=$\sqrt{C{E}^{2}+C{F}^{2}}$=$\sqrt{(2a)^{2}+{a}^{2}}$=$\sqrt{5}$a;
(2)证明:∵AE2+EF2=(2$\sqrt{5}$a)2+($\sqrt{5}$a)2=25a2,AF2=(5a)2=25a2,
∴AE2+EF2=AF2,
∴∠AEF=90°,
即△AEF为直角三角形.
点评 本题考查了正方形的性质、勾股定理、勾股定理的逆定理;熟练掌握正方形的性质,并能进行推理论证与计算是解决问题的关键.


科目:初中数学 来源: 题型:解答题
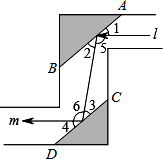 如图是潜望镜工作原理示意图,阴影部分是平行放置在潜望镜里的两面镜子.已知光线经过镜子反射时,有∠1=∠2,∠3=∠4,请解释进入潜望镜的光线l为什么和离开潜望镜的光线m是平行的?
如图是潜望镜工作原理示意图,阴影部分是平行放置在潜望镜里的两面镜子.已知光线经过镜子反射时,有∠1=∠2,∠3=∠4,请解释进入潜望镜的光线l为什么和离开潜望镜的光线m是平行的?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
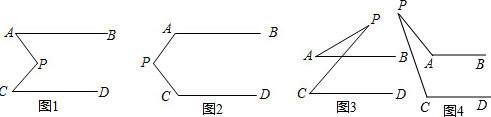
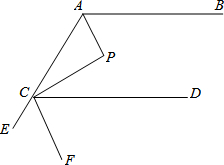 如图,AP,CP分别平分∠BAC,∠ACD,∠P=90°,设∠BAP=α.
如图,AP,CP分别平分∠BAC,∠ACD,∠P=90°,设∠BAP=α.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
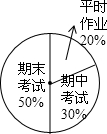 某初中一个学期的数学总平均分是按扇形图信息要求进行计算的,该校胡军同学这个学期的数学成绩如下:则胡军这个学期数学总平均分为( )
某初中一个学期的数学总平均分是按扇形图信息要求进行计算的,该校胡军同学这个学期的数学成绩如下:则胡军这个学期数学总平均分为( ) | 胡军 | 平时作业 | 期中考试 | 期末考试 |
| 90 | 85 | 88 |
| A. | 87.5 | B. | 87.6 | C. | 87.7 | D. | 87.8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 52 | B. | 62 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
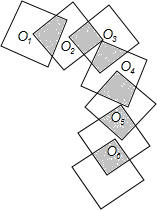 如图,7个正方形的边长均为1,O1、O2、O3、O4、O5、O6是前面六个正方形的中心,同时又是后面六个正方形的顶点,则图中阴影部分的面积是1.5.
如图,7个正方形的边长均为1,O1、O2、O3、O4、O5、O6是前面六个正方形的中心,同时又是后面六个正方形的顶点,则图中阴影部分的面积是1.5.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com