
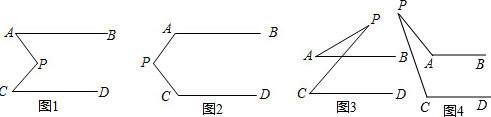
分析 过点P作AB的平行线,用相似的证明方法运用平行线的性质进行证明即可.
解答 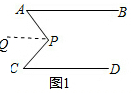 解:如图1,过点P作PQ∥AB,
解:如图1,过点P作PQ∥AB,
∴∠APQ=∠A(两直线平行,内错角相等)
∵PQ∥AB,AB∥CD.
∴PQ∥CD(平行于同一直线的两直线平行)
∴∠CPQ=∠C
∴∠APQ+∠CPQ=∠A+∠C
即∠APC=∠A+∠C,
故两人的证明过程中,完全正确的是小明的证法;
如图2, 过点P作PE∥AB,
过点P作PE∥AB,
∴∠APE+∠A=180°,∠A=120°,∴∠APE=60°,
∵PE∥AB,AB∥CD.
∴PE∥CD(平行于同一直线的两直线平行)
∴∠CPE+∠C=180°,∠C=140°,∴∠CPE=40°,
∴∠APC=∠APE+∠CPE
=100°;
如图3,过点P作PF∥AB,
∴∠APF=∠A,
∵PF∥AB,AB∥CD.
∴PF∥CD,
∴∠CPF=∠C
∴∠CPF-∠APF=∠C-∠A
即∠APC=∠C-∠A=40°;
如图4,过点P作PG∥AB,
∴∠APG+∠A=180°,∴∠APG=180°-∠A
∵PG∥AB,AB∥CD,
∴PG∥CD,(平行于同一直线的两直线平行)
∴∠CPG+∠C=180°,∴∠CPG=180°-∠C
∴∠APC=∠CPG-∠APG=∠A-∠C.
点评 本题考查的是平行线的性质,掌握平行线的性质:两直线平行,同位角相等;两直线平行,内错角相等;两直线平行同旁内角互补是解题的关键.


科目:初中数学 来源: 题型:填空题
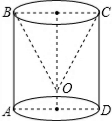 如图,圆柱体内挖去一个与它不等高的圆锥,锥顶O到AD的距离为1,∠OCD=30°,OC=4,则挖去圆锥后的表面积是(16+8$\sqrt{3}$)π.
如图,圆柱体内挖去一个与它不等高的圆锥,锥顶O到AD的距离为1,∠OCD=30°,OC=4,则挖去圆锥后的表面积是(16+8$\sqrt{3}$)π.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
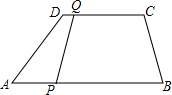 如图,在梯形ABCD中,CD∥AB,且CD=6cm,AB=9cm,P、Q分别从A、C同时出发,P以1cm/s的速度由A向B运动,Q以2cm/s的速度由C向D运动.则2或3秒时,直线QP将四边形ABCD截出一个平行四边形.
如图,在梯形ABCD中,CD∥AB,且CD=6cm,AB=9cm,P、Q分别从A、C同时出发,P以1cm/s的速度由A向B运动,Q以2cm/s的速度由C向D运动.则2或3秒时,直线QP将四边形ABCD截出一个平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
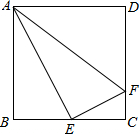 如图,在正方形ABCD中,点E为BC的中点,CF=$\frac{1}{4}$CD,连接AE、AF、EF.设CF=a
如图,在正方形ABCD中,点E为BC的中点,CF=$\frac{1}{4}$CD,连接AE、AF、EF.设CF=a查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
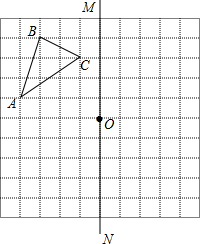 如图,每个小方格都是边长为1个单位长度的小正方形.
如图,每个小方格都是边长为1个单位长度的小正方形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com