
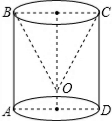
 如图,圆柱体内挖去一个与它不等高的圆锥,锥顶O到AD的距离为1,∠OCD=30°,OC=4,则挖去圆锥后的表面积是(16+8$\sqrt{3}$)π.
如图,圆柱体内挖去一个与它不等高的圆锥,锥顶O到AD的距离为1,∠OCD=30°,OC=4,则挖去圆锥后的表面积是(16+8$\sqrt{3}$)π. 分析 首先过点O作OE⊥CD于点E,利用锐角三角函数关系求出EO,EC的长度,进而得出圆锥侧面积,圆柱底面圆的面积,圆柱侧面积,即可得出挖去后该物体的表面积.
解答 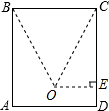 解:过点O作OE⊥CD于点E,
解:过点O作OE⊥CD于点E,
∵∠OCD=30°,OC=4,
∴sin30°=$\frac{OE}{OC}$=$\frac{OE}{4}$,
解得:EO=2,
cos30°=$\frac{EC}{CO}$=$\frac{EC}{4}$=$\frac{\sqrt{3}}{2}$,
解得:EC=2$\sqrt{3}$,
故由题意可得出:圆锥底面半径为2,DC=1+EC=1+2$\sqrt{3}$,
则圆锥侧面积为:S=π×底面圆的半径×母线=π×2×4=8π,圆柱底面圆的面积为:π×2 2=4π,
圆柱侧面积为:底面圆的周长×圆柱的高=2×π×2×(1+2$\sqrt{3}$)=4π+8$\sqrt{3}$π,
故该物体的表面积=圆锥侧面积+圆柱底面圆的面积+圆柱侧面积=8π+4π+4π+8$\sqrt{3}$π=(16+8$\sqrt{3}$)π.
故答案为:(16+8$\sqrt{3}$)π.
点评 此题主要考查了圆锥的有关计算以及圆柱侧面积求法和锐角三角函数的应用等知识,根据图象得出该物体的表面积=圆锥侧面积+圆柱底面圆的面积+圆柱侧面积是解题关键.


科目:初中数学 来源: 题型:选择题
| A. | 对角线相等的四边形是矩形 | |
| B. | 对角线互相垂直的四边形是菱形 | |
| C. | 对角线互相平分的四边形是平行四边形 | |
| D. | 对角线平分每一组对角的四边形是正方形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
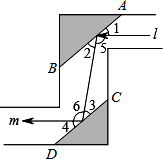 如图是潜望镜工作原理示意图,阴影部分是平行放置在潜望镜里的两面镜子.已知光线经过镜子反射时,有∠1=∠2,∠3=∠4,请解释进入潜望镜的光线l为什么和离开潜望镜的光线m是平行的?
如图是潜望镜工作原理示意图,阴影部分是平行放置在潜望镜里的两面镜子.已知光线经过镜子反射时,有∠1=∠2,∠3=∠4,请解释进入潜望镜的光线l为什么和离开潜望镜的光线m是平行的?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
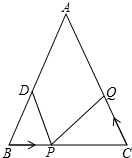 如图,AB=AC=10cm,BC=8cm,点D为AB的中点,点P在线段BC上以3cm/秒的速度由点B向点C运动,同时,点Q在线段CA上由C点向A点运动.
如图,AB=AC=10cm,BC=8cm,点D为AB的中点,点P在线段BC上以3cm/秒的速度由点B向点C运动,同时,点Q在线段CA上由C点向A点运动.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
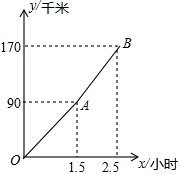 “五一节”期间,小华一家自驾游去了离家170千米的某地,如图是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.下列结论:
“五一节”期间,小华一家自驾游去了离家170千米的某地,如图是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.下列结论:| A. | ①② | B. | ③④ | C. | ①②③ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
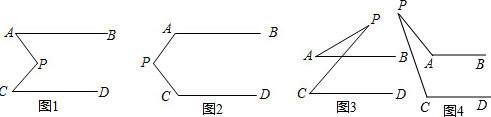
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com