
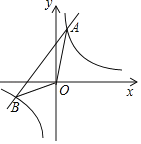
【题目】如图,点A、B是双曲线y=![]() (k为正整数)与直线AB的交点,且A、B两点的横坐标是关于x的方程:x2+kx﹣k﹣1=0的两根
(k为正整数)与直线AB的交点,且A、B两点的横坐标是关于x的方程:x2+kx﹣k﹣1=0的两根
(1)填表:
k | 1 | 2 | 3 | … | n(n为正整数) |
A点的横坐标 |
|
|
|
|
|
B点的横坐标 |
|
|
|
|
|
(2)当k=n(n为正整数)时,试求直线AB的解析式(用含n的式子表示);
(3)当k=1、2、3、…n时,△ABO的面积,依次记为S1、S2、S3…Sn,当Sn=40时,求双曲线y=![]() 的解析式.
的解析式.
【答案】(1)1,1,1,…,1;﹣2,﹣3,﹣4,…,﹣n﹣1(2)y=x+n(3)y=![]()
【解析】
(1)根据k的值,即可得到一元二次方程的解,进而得到A点的横坐标,B点的横坐标;(2)根据当k=n(n为正整数)时,A点的横坐标为1,B点的横坐标为﹣n﹣1,可得A(1,n+1),B(﹣n﹣1,﹣1),运用待定系数法即可得出直线AB的解析式;(3)先求得直线AB与y轴交于(0,n),再根据当Sn=40时,![]() ×n(n+1+1)=40,即可得到n=8,进而得出A(1,9),据此可得双曲线的解析式为y=
×n(n+1+1)=40,即可得到n=8,进而得出A(1,9),据此可得双曲线的解析式为y=![]() .
.
(1)当k=1时,方程x2+x﹣2=0的解为:x1=1,x2=﹣2;
当k=2时,方程x2+2x﹣3=0的解为:x1=1,x2=﹣3;
k=3时,方程x2+3x﹣4=0的解为:x1=1,x2=﹣4;
k=n时,方程x2+nx﹣n﹣1=0的解为:x1=1,x2=﹣n﹣1;
∵点A在第一象限,点B在第三象限,
∴A点的横坐标依次为:1,1,1,…,1;
B点的横坐标依次为:﹣2,﹣3,﹣4,…,﹣n﹣1;
故答案为:1,1,1,…,1;﹣2,﹣3,﹣4,…,﹣n﹣1;
(2)当k=n(n为正整数)时,A点的横坐标为1,B点的横坐标为﹣n﹣1,
令x=1,则y=![]() =n+1;
=n+1;
令x=﹣n﹣1,则y=![]() =﹣1;
=﹣1;
∴A(1,n+1),B(﹣n﹣1,﹣1),
设直线AB的解析式为y=px+q,则
![]() ,
,
解得![]() ,
,
∴直线AB的解析式为y=x+n;
(3)∵直线y=x+n中,令x=0,则y=n,即直线AB与y轴交于(0,n),
∴当Sn=40时,![]() ×n(n+1+1)=40,
×n(n+1+1)=40,
解得n=8(负值已舍去),
∴A(1,9),
∴双曲线的解析式为:y=![]() .
.


科目:初中数学 来源: 题型:
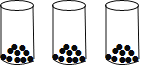
【题目】如图,在三个小桶中装有数量相同的小球(每个小桶中至少有三个小球),
第一次变化:从左边小桶中拿出两个小球放入中间小桶中;
第二次变化:从右边小桶中拿出一个小球放入中间小桶中;
第三次变化:从中间小桶中拿出一些小球放入右边小桶中,使右边小桶中小球个数是最初的两倍.
(1)若每个小桶中原有3个小球,则第一次变化后,中间小桶中小球个数是左边小桶中小球个数的____倍;
(2)若每个小桶中原有a个小球,则第二次变化后中间小桶中有_____个小球(用a表示);
(3)求第三次变化后中间小桶中有多少个小球?
查看答案和解析>>
科目:初中数学 来源: 题型:
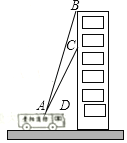
【题目】贵阳市某消防支队在一幢居民楼前进行消防演习,如图所示,消防官兵利用云梯成功救出在C处的求救者后,发现在C处正上方17米的B处又有一名求救者,消防官兵立刻升高云梯将其救出,已知点A与居民楼的水平距离是15米,且在A点测得第一次施救时云梯与水平线的夹角∠CAD=60°,求第二次施救时云梯与水平线的夹角∠BAD的度数(结果精确到1°).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+x+6及一次函数y=﹣x+m,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新函数(如图所示),请你在图中画出这个新图象,当直线y=﹣x+m与新图象有4个交点时,m的取值范围是( )
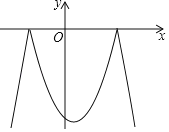
A. ﹣![]() <m<3 B. ﹣
<m<3 B. ﹣![]() <m<2 C. ﹣2<m<3 D. ﹣6<m<﹣2
<m<2 C. ﹣2<m<3 D. ﹣6<m<﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
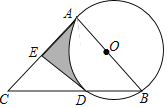
【题目】如图,AB是⊙O的直径,AC是⊙O的切线,切点为A,BC交⊙O于点D,点E是AC的中点.
(1)试判断直线DE与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为2,∠B=50°,AC=4.8,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“垃圾分类”,环保部门要求垃圾要按A,B,C,D四类分别装袋、投放,其中A类指废电池,过期药品等有毒垃圾,B类指剩余食品等厨余垃圾,C类指塑料、废纸等可回收物,D类指出其他垃圾,小明、小亮各投放了一袋垃圾.
(1)直接写出小明投放的垃圾恰好是A类的概率;
(2)求小亮投放的垃圾与小明投放的垃圾是同一类的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | … | ﹣6 | 0 | 4 | 6 | 6 | … |
从上表可知,下列说法正确的有多少个
①抛物线与x轴的一个交点为(﹣2,0);
②抛物线与y轴的交点为(0,6);
③抛物线的对称轴是直线x=![]() ;
;
④抛物线与x轴的另一个交点为(3,0);
⑤在对称轴左侧,y随x增大而减少.
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
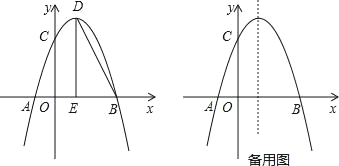
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于点A和点B(3,0),与y轴交于点C(0,3),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接DB.
(1)求此抛物线的解析式及顶点D的坐标;
(2)点M是抛物线上的动点,设点M的横坐标为m.
①当∠MBA=∠BDE时,求点M的坐标;
②过点M作MN∥x轴,与抛物线交于点N,P为x轴上一点,连接PM,PN,将△PMN沿着MN翻折,得△QMN,若四边形MPNQ恰好为正方形,直接写出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
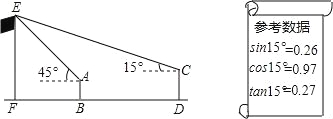
【题目】某校九(18)班开展数学活动,毓齐和博文两位同学合作用测角仪测量学校的旗杆,毓齐站在B点测得旗杆顶端E点的仰角为45°,博文站在D(D点在直线FB上)测得旗杆顶端E点仰角为15°,已知毓齐和博文相距(BD)30米,毓齐的身高(AB)1.6米,博文的身高(CD)1.75米,求旗杆的高EF的长.(结果精确到0.1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com