
【题目】数学活动课上,小聪同学摆弄着自己刚购买的一套三角板,将两块直角三角板的直角顶点C叠放在一起,然后转动三角板,在转动过程中,请解决以下问题: 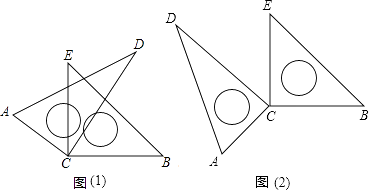
(1)如图(1):当∠DCE=30°时,∠ACB+∠DCE等于多少?若∠DCE为任意锐角时,你还能求出∠ACB与∠DCE的数量关系吗?若能,请求出;若不能,请说明理由.
(2)当转动到图(2)情况时,∠ACB与∠DCE有怎样的数量关系?请说明理由.
【答案】
(1)解:∠ACB+∠DCE=180°;
若∠DCE为任意锐角时,∠ACB+∠DCE=180°,
理由如下:∵∠ACE+∠DCE=90°,
∠BCD+∠DCE=90°,
∴∠ACB+∠DCE=∠ACE+∠DCE+∠BCD+∠DCE=90°+90°=180°
(2)解:∠ACB+∠DCE=180°.
理由如下:∵∠ACD=90°=∠ECB,∠ACD+∠ECB+∠ACB+∠DCE=360°,
∴∠ECD+∠ACB=360°﹣(∠ACD+∠ECB)=360°﹣180°=180°
【解析】(1)当∠DCE=30°时,利用互余计算出∠BCD,然后可得到∠ACB+∠DCE的度数;若∠DCE为任意锐角时,利用∠ACE+∠DCE=90°,∠BCD+∠DCE=90°,然后计算出∠ACB+∠DCE=180°;(2)利用周角定义得到∠ACD+∠ECB+∠ACB+∠DCE=360°所以∠ECD+∠ACB=360°﹣(∠ACD+∠ECB)=180°.
【考点精析】掌握余角和补角的特征是解答本题的根本,需要知道互余、互补是指两个角的数量关系,与两个角的位置无关.


科目:初中数学 来源: 题型:
【题目】化简求值
(1)若a2﹣4a+b2﹣10b+29=0,求a2b+ab2的值
(2)先化简,再求值:(3x+2)(3x﹣2)﹣5x(x﹣1)﹣(2x﹣1)2 , 其中 ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①表示的是某综合商场今年1~5月的商品各月销售总额的情况,图②表示的是商场服装部各月销售额占商场当月销售总额的百分比情况,观察图①、图②,解答下列问题: 
(1)来自商场财务部的数据报告表明,商场1~5月的商品销售总额一共是410万元,请你根据这一信息将图①中的统计图补充完整;
(2)商场服装部5月份的销售额是多少万元?
(3)小刚观察图②后认为,5月份商场服装部的销售额比4月份减少了.你同意他的看法吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,线段AD=10cm,点B,C都是线段AD上的点,且AC=7cm,BD=4cm,若E,F分别是线段AB,CD的中点,求BC与EF的长度. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答
(1)如图,在直线m的同侧有A,B两点,在直线m上找点P,Q,使PA+PB最小,|QB﹣QA|最大(保留作图痕迹) 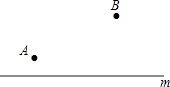
(2)平面直角坐标系内有两点A(2,3),B(4,5),请分别在x轴,y轴上找点P,Q,使PA+PB最小,|QB﹣QA|最大,则点P,Q的坐标分别为 ,
(3)代数式 ![]() +
+ ![]() 的最小值是 , 此时x=
的最小值是 , 此时x=
(4)代数式 ![]() ﹣
﹣ ![]() 的最大值是 , 此时x= .
的最大值是 , 此时x= .
查看答案和解析>>
科目:初中数学 来源: 题型:
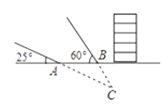
【题目】某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5, ![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按科学记算器MODE MODE 1,使显示器显示D后,求sin90°的值,以下按键顺序正确的是( )
A.sin , 9=
B.9,sin=
C.sin , 9,0=
D.9,0=
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com