
【题目】解答
(1)如图,在直线m的同侧有A,B两点,在直线m上找点P,Q,使PA+PB最小,|QB﹣QA|最大(保留作图痕迹) 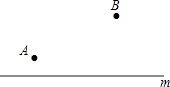
(2)平面直角坐标系内有两点A(2,3),B(4,5),请分别在x轴,y轴上找点P,Q,使PA+PB最小,|QB﹣QA|最大,则点P,Q的坐标分别为 ,
(3)代数式 ![]() +
+ ![]() 的最小值是 , 此时x=
的最小值是 , 此时x=
(4)代数式 ![]() ﹣
﹣ ![]() 的最大值是 , 此时x= .
的最大值是 , 此时x= .
【答案】
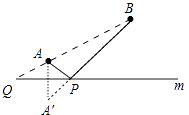
(1)解:①作点A关于直线m的对称点A′,连接A′B与直线m交于点P,此时PA+PB最小,点P如图所示.
②延长BA交直线m于Q,此时,|QB﹣QA|最大,点Q如图所示.
(2)( ![]() ,0);(0,1)
,0);(0,1)
(3)10;![]()
(4)2;﹣1
【解析】解(2)点A关于x轴的对称点A′(2,﹣3),
直线A′B的解析式为y=4x﹣11,y=0时,x= ![]() ,
,
所以点P坐标( ![]() ,0).
,0).
直线AB解析式为y=x+1,与y轴的交点为(0,1),
所以点Q坐标(0,1).
所以答案是( ![]() ,0),(0,1)
,0),(0,1)
3)∵ ![]() +
+ ![]() =
= ![]() +
+ ![]() ,
,
欲求 ![]() +
+ ![]() 的最小值,
的最小值,
可以看作在x轴上找一点P,使得点P到(4,5),(2,3)的距离之和最小,
由(2)可知x= ![]() ,最小值=
,最小值= ![]() =10,
=10,
所以答案是10, ![]() .
.
4)∵ ![]() ﹣
﹣ ![]() ═
═ ![]() ﹣
﹣ ![]() ,
,
欲求 ![]() ﹣
﹣ ![]() 的最大值,
的最大值,
可以看作在x轴上找一点Q,使得Q到A(2,3),B(4,5)的距离之和最大,
∵直线AB解析式为y=x+1,与x轴交于点Q(﹣1,0),
∴x=﹣1时,此时最大值=2 ![]() .
.
所以答案是2 ![]() ,﹣1.
,﹣1.
【考点精析】解答此题的关键在于理解轴对称-最短路线问题的相关知识,掌握已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 相等的圆心角所对的弧相等B. 三角形的内心到三角形三个顶点距离相等
C. 等弧所对的弦相等D. 圆的切线垂直于半径
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P(-2,-3)向左平移1个单位,再向上平移3个单位,则所得到的点的坐标为( )
A.(-3,0) B.(-1,6) C.(-3,-6) D.(-1,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动课上,小聪同学摆弄着自己刚购买的一套三角板,将两块直角三角板的直角顶点C叠放在一起,然后转动三角板,在转动过程中,请解决以下问题: 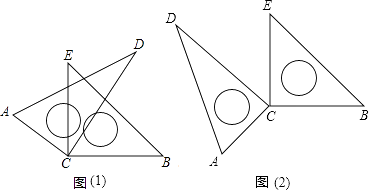
(1)如图(1):当∠DCE=30°时,∠ACB+∠DCE等于多少?若∠DCE为任意锐角时,你还能求出∠ACB与∠DCE的数量关系吗?若能,请求出;若不能,请说明理由.
(2)当转动到图(2)情况时,∠ACB与∠DCE有怎样的数量关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:①三点确定一个圆;②相等的圆周角所对的弧相等;③平分弦的直径垂直于弦;④等弧所对的圆心角相等;其中真命题的个数是 ( )
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
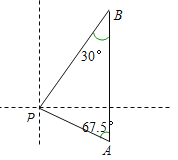
【题目】马航MH370 客机“失联”,我国“海巡01号”前往搜寻。如图某天上午9时,“海巡01号” 轮船位于A处,观测到某小岛P位于轮船的北偏西67.5°,轮船以21海里/时的速度向正北方向行驶,下午2时该船到达B处,这时观测到小岛P位于该船的南偏西30°方向,求此时轮船所处位置B与小岛P的距离?(精确到0.1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com