
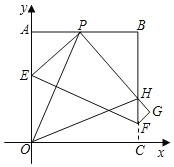
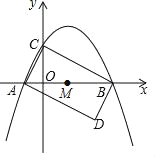
����Ŀ����ͼ����һ�ű߳�Ϊ8��������ֽƬOABC����ֱ������ϵ�У�ʹ��OA��y���غϣ�OC��x���غϣ���PΪ������AB���ϵ�һ��(�����A����B�غ�)����������ֽƬ�۵���ʹ��O����P������C����G����PG��BC��H���ۺ�ΪEF������OP��OH��
����̽��
��1����AP=4ʱ
��ֱ��д����E����������������
����ֱ��EF�ĺ�������ʽ��
����̽��
��2������P�ڱ�AB���ƶ�ʱ����APO���OPH�Ķ���������ȣ���˵�����ɣ�
��չӦ��
��3������P�ڱ�AB���ƶ�ʱ����PBH���ܳ��Ƿ����仯����֤����Ľ��ۣ�
���𰸡���1����(0��5)����![]() ����2�����ɼ���������3���ܳ�=16�����ᷢ���仯��֤����������
����2�����ɼ���������3���ܳ�=16�����ᷢ���仯��֤����������
��������
��1�����裺OE��PE��a����AE��8��a��AP��4����Rt��AEP�У��ɹ��ɶ����ã�PE2��AE2+AP2��������⣻
��֤����AOP�ա�FRE��AAS������ER��AP��4���ʵ�F��8��1����������⣻
��2����EOP����EPO������EPH����EOC��90�����ʡ�EPH����EPO����EOC����EOP������POC����OPH������ΪAB��OC���ʡ�APO����POC��������⣻
��3��֤����AOP�ա�QOP��AAS������OCH�ա�OQH��SAS������CH��QH��������⣮
��1�����裺OE=PE=a����AE=8��a��AP=4��
��Rt��AEP�У��ɹ��ɶ����ã�PE2=AE2+AP2��
��a2=(8��a)2+16����ã�a=5��
�ʵ�E(0��5)��
�ʴ�Ϊ��(0��5)��
������F��FR��y���ڵ�R��
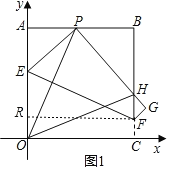
�۵����O����P�������O��P����ֱ��EF�Գƣ���OP��EF��
���EFR+��FER=90��������FER+��AOP=90����
���AOP=��EFR��
����OAP=��FRE��RF=AO��
���AOP�ա�FRE(AAS)��
��ER=AP=4��
OR=EO��OR=5��4=1���ʵ�F(8��1)��
����E��F���������һ�κ�������ʽ��y=kx+b
�ã�![]() ����ã�
����ã�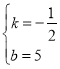 ��
��
��ֱ��EF�ı���ʽΪ��y=��![]() x+5��
x+5��
��2����PE=OE��
���EOP=��EPO��
���ߡ�EPH=��EOC=90����
���EPH����EPO=��EOC����EOP��
����POC=��OPH��
����AB��OC��
���APO=��POC��
���APO=��OPH��
��3����ͼ����O��OQ��PH������ΪQ��
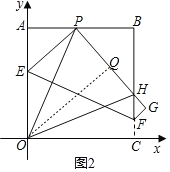
�ɣ�1��֪��APO=��OPH��
����AOP����QOP��
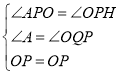
���AOP�ա�QOP(AAS)��
��AP=QP��AO=OQ��
����AO=OC��
��OC=OQ��
���ߡ�C=��OQH=90����OH=OH��
���OCH�ա�OQH(SAS)��
��CH=QH��
���PHB���ܳ�=PB+BH+PH=AP+PB+BH+HC=AB+CB=16��
�ʴ�Ϊ��16��


 ����˼ά�żӿ���ϵ�д�
����˼ά�żӿ���ϵ�д� �����Ծ�ϵ�д�
�����Ծ�ϵ�д� �ο�����������100��ϵ�д�
�ο�����������100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�����ͬѧ����������������Ϸ���̶�����������ƹ�����������1���ܣ��ƹ�![]() ���ܻص������ߣ���ͼʾ����;��ƹ���������ʱ����ص����������ܣ��������ͬѧ�����ļ����������˷���6���ӣ���ͬѧ��˳�����ꣻ�º�ͬѧ˵�����������õ�ȫ��ʱ��ĺ�Ϊ50��������ͬѧ˵��������̲�������ʱ�����ٶ����ҵ�1.2��������ͼ����Ϣ������������õ�ʱ�䣮
���ܻص������ߣ���ͼʾ����;��ƹ���������ʱ����ص����������ܣ��������ͬѧ�����ļ����������˷���6���ӣ���ͬѧ��˳�����ꣻ�º�ͬѧ˵�����������õ�ȫ��ʱ��ĺ�Ϊ50��������ͬѧ˵��������̲�������ʱ�����ٶ����ҵ�1.2��������ͼ����Ϣ������������õ�ʱ�䣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
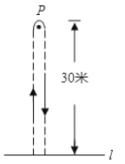
����Ŀ����ͼ����ABC�У���ACB��90����AC��4��BC��3����P��AB����һ������
����PCB�ǵ���������ʱ����AP�ij���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ȱ������εĶ���A(1��1)��B(3��1)���涨�ѵȱߡ�ABC������y�ᷭ�ۣ�������ƽ��1����λ��Ϊһ�α任�����������������2020�α任�ȱߡ�ABC�Ķ���C������Ϊ____��
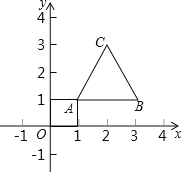
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
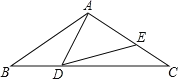
����Ŀ����ͼ���ڡ�ABC�У�AB=AC=2����B=36�㣬��D���߶�BC���˶�(��D�����B��C�غ�)������AD������ADE=36�㣬DE���߶�AC�ڵ�E��
��1������BDA=128��ʱ����EDC=������������AED=����������
��2���߶�DC�ij���Ϊ��ֵʱ����ABD�ա�DCE����˵�����ɣ�
��3���ڵ�D���˶������У���ADE����״�����ǵ����������������ԣ���ֱ��д����BDA�Ķ������������ԣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�ܳ�25�����ӣ�б������ֱ��ǽ�ϣ���ʱ���ӵ���ǽ7�ף�
��1����ʱ���Ӷ������������ף�
��2�������Ӷ����»�4�ף���ô���ӵ˽����������ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2+bx+2��x���ཻ��A����1��0����B��4��0�����㣬��y���ཻ�ڵ�C��
��1���������ߵĽ���ʽ��
��2������ABC��AB�е�M��ת180�����õ���BAD��
�����D�����ꣻ
���ж��ı���ADBC����״����˵�����ɣ�
��3���ڸ������߶Գ������Ƿ���ڵ�P��ʹ��BMP���BAD���ƣ������ڣ��������������������P������ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+c��x�ύ�ڵ�A��-1��0�����������꣨1��n����y��Ľ����ڣ�0��2������0��3��֮�䣨�����˵㣩�������н��ۣ���3a+b<0����-1��a��-![]() ���۶�������ʵ��m��a+b��am2+bm�ܳ������ܹ���x�ķ���ax2+bx+c=n-1����������ȵ�ʵ���������н�����ȷ�ĸ���Ϊ( )
���۶�������ʵ��m��a+b��am2+bm�ܳ������ܹ���x�ķ���ax2+bx+c=n-1����������ȵ�ʵ���������н�����ȷ�ĸ���Ϊ( )

A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�����������ڴ�����������һ������������Ȧ�� 2��2�������� 1��2��8��9���� ���Ȧ�����ĸ����е���С����������Ļ�Ϊ 308����ô���ĸ����ĺ�Ϊ�� ��
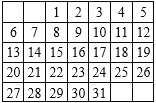
A.68B.72C.74D.76
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com