
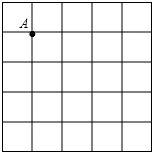
 ��ͼ����5��5�������������У�ÿ��С�����εı߳�����1�������������а�����Ҫ��ͼ�Σ�
��ͼ����5��5�������������У�ÿ��С�����εı߳�����1�������������а�����Ҫ��ͼ�Σ����� ��1�����ݹ��ɶ�����֪ʹ�߶�ABΪֱ�DZ�Ϊ2��1��ֱ�������ε�б���ɣ�
��2���������������߳��ֱ���3��2$\sqrt{2}$��������ABC���ɣ�
��3�����������ε������ʽ���ɵõ�������������ABC��AB���ϸ��߳���
��� 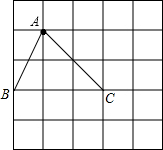 �⣺��1����ͼ��ʾ��
�⣺��1����ͼ��ʾ��
��2����ͼ��ʾ��
��3��������ABC��AB���ϸ��߳�Ϊ��$\frac{1}{2}$��3��2��2��$\sqrt{5}$
=3��2��$\sqrt{5}$
=$\frac{6\sqrt{5}}{5}$��
�ʴ�Ϊ��$\frac{6\sqrt{5}}{5}$��
���� ���⿼���˹��ɶ���������Ҫ������ĿҪ����ƻ�ͼ����Ҳ�Ƚ���Ŀ������ѧ����������������������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��AB��CD��EF����CG��AF����ͼ�����CGE��ȵĽǹ��У�����������
��ͼ��AB��CD��EF����CG��AF����ͼ�����CGE��ȵĽǹ��У�����������| A�� | 3 | B�� | 4 | C�� | 5 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
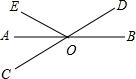 ��ͼ����ֱ֪��AB��CD�ཻ��O�㣬OAƽ�֡�EOC����EOC=60�㣬���BOD=30�㣮
��ͼ����ֱ֪��AB��CD�ཻ��O�㣬OAƽ�֡�EOC����EOC=60�㣬���BOD=30�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com