
分析 (1)(2)根据阅读材料可以得到可以把三项式中的两项作为完全平方式的两项,从而确定第三项即可;
(3)首先分组利用完全平方公式分解因式,利用非负数的性质求得a、b、c的数值,进一步求得a+b+c的值即可.
解答 解:(1)x2-4x+9的三种配方分别为:
x2-4x+9=(x-2)2+5;
x2-4x+9=(x+3)2-10x;
x2-4x+9=(x-3)2+2x(或x2-4x+9=${({\frac{2}{3}x-3})^2}+\frac{5}{9}{x^2}$);
(2)a2+ab+b2=(a+b)2-ab;
或a2+ab+b2=(a+$\frac{1}{2}$b)2+$\frac{3}{4}$b2;
或a2+ab+b2=(a-b)2+3ab;
或a2+ab+b2=(a+b)2-ab;
或a2+ab+b2=${({a+\frac{1}{2}b})^2}+\frac{3}{4}{b^2}$${({\frac{1}{2}a+b})^2}+\frac{3}{4}{a^2}$;
(3)a2+b2+c2-ab-3b-2c+4=0
a2-ab+$\frac{1}{4}$b2+$\frac{3}{4}$(b2-4b+4)+c2-2c+1=0
(a-$\frac{1}{2}$b)2+$\frac{3}{4}$(b-2)2+(c-1)2=0
∴a-$\frac{1}{2}$b=0,$\frac{3}{4}$(b-2)=0,c-1=0
∴a=1,b=2,c=1,
则a+b+c=4.
点评 本题考查了完全平方式,正确读懂题目中的阅读材料,理解配方的方法是关键.另外,注意分组的技巧和方法.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
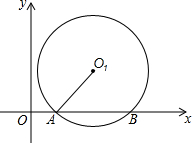 如图,⊙O1与x轴交于A(1,0),B(5,0)两点,⊙O1的半径为3.
如图,⊙O1与x轴交于A(1,0),B(5,0)两点,⊙O1的半径为3.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 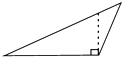 | B. | 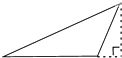 | C. | 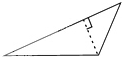 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
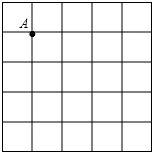 如图,在5×5的正方形网格中,每个小正方形的边长都是1,在所给网格中按下列要求画出图形:
如图,在5×5的正方形网格中,每个小正方形的边长都是1,在所给网格中按下列要求画出图形:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com