
课本回顾
如图,用半径R=3cm,r=2cm的钢球测量口小内大的内孔的直径D.测得钢球顶点与孔口平面的距离分别为a=4cm,b=2cm,则内孔直径D的大小为 .
问题拓展
如图,在矩形ABCD内,已知⊙O1与⊙O2互相外切,且⊙O1与边AD、DC相切,⊙O2与边AB、BC相切.若AB=4,BC=3,⊙O1与⊙O2的半径分别为r,R.求O1O2的值.
灵活运用
如图,某市民广场是半径为60米,圆心角为90°的扇形AOB,广场中两个活动场所是圆心在OA、OB上,且与扇形OAB内切的半圆☉O1、☉O2,其余为花圃.若这两个半圆相外切,试计算当两半圆半径之和为50米时活动场地的面积.

(1)9cm;(2)7-2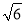 ;(3)650π平方米.
;(3)650π平方米.
【解析】
试题分析:(1)利用相切两圆的性质得出AB=5cm,再利用已知得出BC的长,由勾股定理求出AC的长,即可得出EF的长;
(2)连接O1、O2,并分别过O1、O2作AB、BC的平行线,则O1O22=O1 E2+O2E2,进而求出R+r的值即可;
(3)当两圆半径之和为50米时,有O1O=60-r,O2O=60-R,O1O2=50,则(60-r)2+(60-R)2=502,即可得出R2+r2,进而利用圆的面积公式求出即可.
(1)如图1,
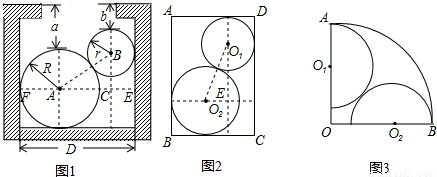
∵半径R=3cm,r=2cm,a=4cm,b=2cm,
∴AB=5cm,BC=3+4-4=3(cm),
∴AC=4cm,
∴D=EF=AF+EC+AC=3+4+2=9(cm).
(2)如图2,连接O1、O2,并分别过O1、O2作AB、BC的平行线.
则O1O22=O1 E2+O2E2.
即(R+r)2=[4-(R+r)]2+[3-(R+r)]2
化简得:(R+r)2-14(R+r)+25=0,
解得:O1O2=r+R=7-2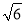 或7+2
或7+2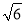 (不合题意舍去);
(不合题意舍去);
(3)当两圆半径之和为50米时,
有O1O=60-r,O2O=60-R,O1O2=50,
则(60-r)2+(60-R)2=502.
即R2+r2-120(R+r)+4700=0.
∴R2+r2=1300.
∴活动场所面积=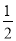 πR2+
πR2+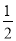 πr2=
πr2=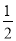 π•1300=650π(平方米).
π•1300=650π(平方米).
考点:圆的综合题.


科目:初中数学 来源:2013-2014学年江苏省太仓市九年级5月学科教学质量调研数学试卷(解析版) 题型:填空题
如图,AB是⊙O的直径,C,D两点在⊙O上,若∠BCD=40°,则∠ABD的度数为 °.[来

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省南京市溧水区中考一模数学试卷(解析版) 题型:填空题
已知菱形ABCD的对角线相交于点O,AC=6cm,BD=8cm,则菱形的高AE为 cm.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省南京市溧水区中考一模数学试卷(解析版) 题型:选择题
一次函数y=kx+b与反比例函数y= 的图象如图所示,下列结论正确的是
的图象如图所示,下列结论正确的是
A.它们的函数值y随着x的增大而增大
B.它们的函数值y随着x的增大而减小
C.k<0
D.它们的自变量x的取值为全体实数

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省南京市六合区中考一模数学试卷(解析版) 题型:解答题
桌面上有5张背面相同的卡片,正面分别写着数字“1”、“2”、“3”、“4”、 “5”.将卡片背面朝上洗匀.
(1)小军从中任意抽取一张,抽到偶数的概率是 ;
(2)小红从中同时抽取两张.规定:抽到的两张卡片上的数字之和为奇数,则小军胜,否则小红胜.你认为这个游戏公平吗?请用树状图或表格说明你的理由.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省南京市六合区中考一模数学试卷(解析版) 题型:填空题
甲、乙两名射击运动员在某场测试中各射击20次,测试成绩如下表:
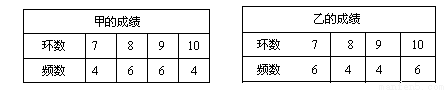
则 (选填甲、乙)运动员测试成绩更稳定.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省兴化市九年级中考网上阅卷适应性训练(即一模)数学试卷(解析版) 题型:解答题
如图,在平面直角坐标系中,反比例函数 的图象和矩形ABCD在第二象限,AD平行于x轴,且AB=2,AD=4,点C的坐标为(-2,4).
的图象和矩形ABCD在第二象限,AD平行于x轴,且AB=2,AD=4,点C的坐标为(-2,4).
(1)直接写出A、B、D三点的坐标;
(2)若将矩形只向下平移,矩形的两个顶点恰好同时落在反比例函数的图象上,求反比例函数的解析式和此时直线AC的解析式y=mx+n.并直接写出满足 的x取值范围.
的x取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com