
【题目】如图,AB是⊙O的直径, BM切⊙O于点B,点P是⊙O上的一个动点(不经过A,B两点),过O作OQ∥AP交![]() 于点Q,过点P作
于点Q,过点P作![]() 于C,交
于C,交![]() 的延长线于点E,连结
的延长线于点E,连结![]() .
.
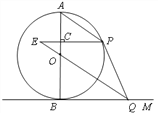
(1)求证:PQ与⊙O相切;
(2)若直径AB的长为12,PC=2EC,求tan∠E的值.
【答案】(1)详见解析;(2)![]() .
.
【解析】试题分析:(1)连接OP,根据平行线的性质得到∠EOC=∠OAP,∠POQ=∠APO,根据等腰三角形的性质得到∠APO=∠OAP,推出△POQ≌△BOQ,根据全等三角形的性质得到∠OPQ=∠OBQ=90°,根据切线的判定定理即可得到结论;
(2)由OQ∥AP,可得△COE∽△CAP,从而列比例式![]() 求出PC的长; 由OQ∥AP,∠E=∠APC,所以tan∠E=
求出PC的长; 由OQ∥AP,∠E=∠APC,所以tan∠E=![]() ,从而求得结果.
,从而求得结果.
解:(1)连接OP,
∵OQ∥AP,∴∠A=∠BOQ,∠APO=∠POQ,
又∵OA=OP,∴∠A=∠APO.
∴∠BOQ=∠POQ,
在△OQB与△OQP中,
∠BOQ=∠POQ,OP=OB,OQ=OQ,
∴△OQB≌△OQP,
∴∠OBQ=∠OPQ,PQ=BQ.
∵BM切⊙O于点B,∴∠OBQ=∠OPQ=90°.
∴PQ与⊙O相切;
(2) ∵OQ∥AP,∴△COE∽△CAP,∴![]() ,
,
由AB的长为12,
∴OA=6.
∵PC=2EC, ∴OC=2,AC=4,
∴![]() .
.
由OQ∥AP,∠E=∠APC,
∴tan∠E=![]() .
.


科目:初中数学 来源: 题型:
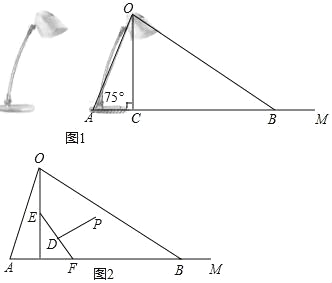
【题目】如图1为放置在水平桌面上的台灯的平面示意图,灯臂AO长为50cm,与水平桌面所形成的夹角∠OAM为75°.由光源O射出的边缘光线OC,OB与水平桌面所形成的夹角∠OCA,∠OBA分别为90°和30°.(不考虑其他因素,结果精确到0.1cm. sin75°≈0.97,cos75°≈0.26,![]() ≈1.73
≈1.73
(1)求该台灯照亮水平桌面的宽度BC.
(2)人在此台灯下看书,将其侧面抽象成如图2所示的几何图形,若书与水平桌面的夹角∠EFC为60°,书的长度EF为24cm,点P为眼睛所在位置,当点P在EF 的垂直平分线上,且到EF距离约为34cm(人的正确看书姿势是眼睛离书距离约1尺≈34cm)时,称点P为“最佳视点”.请通过计算说明最佳视点P在不在灯光照射范围内?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,![]() ,
,![]() .点G,E分别在边AB,CD上,点F,H在对角线AC上.若四边形EFGH是菱形,则AG的长是( )
.点G,E分别在边AB,CD上,点F,H在对角线AC上.若四边形EFGH是菱形,则AG的长是( )

A.![]() B.5C.
B.5C.![]() D.6
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,EF与AB,CD分别交于点G,H,∠CHG的平分线HM交AB于点M,若∠EGB=50°,则∠GMH的度数为( )

A. 50°B. 55°C. 60°D. 65°
查看答案和解析>>
科目:初中数学 来源: 题型:
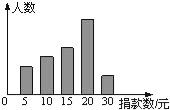
【题目】某校学生会干部对校学生会倡导的“助残”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,下图是根据这组数据绘制的统计图,图中从左到右各长方形高度之比为3:4:5:8:2,又知此次调查中捐15元和20元的人数共39人.
(1)他们一共抽查了多少人捐款数不少于20元的概率是多少?
(2)这组数据的众数、中位数各是多少?
(3)若该校共有2310名学生,请估算全校学生共捐款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,E、F分别是AB、CD的中点.
(1)求证:四边形EBFD为平行四边形;
(2)对角线AC分别与DE、BF交于点M、N.求证:△ABN≌△CDM.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进甲、乙两种商品,已知每件甲种商品的价格比每件乙种商品的价格贵10元,用350元购买甲种商品的件数恰好与用300元购买乙种商品的件数相同.
(1)求甲、乙两种商品每件的价格各是多少元?
(2)计划购买这两种商品共50件,且投入的经费不超过3200元,那么,最多可购买多少件甲种商品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,梯形ABCD中,AD∥BC,∠C=90°,BA=BC.动点E、F同时从点B出发,点E沿折线 BA–AD–DC运动到点C时停止运动,点F沿BC运动到点C时停止运动,它们运动时的速度都是1 cm/s.设E出发t s时,△EBF的面积为y cm2.已知y与t的函数图象如图②所示,其中曲线OM为抛物线的一部分,MN、NP为线段.
请根据图中的信息,解答下列问题:
(1)AD= cm,BC= cm;
(2)求a的值,并用文字说明点N所表示的实际意义;
(3)直接写出当自变量t为何值时,函数y的值等于5.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个三位数,十位数字是![]() ,百位数字是十位数字的2倍,个位数字比十位数字小2.
,百位数字是十位数字的2倍,个位数字比十位数字小2.
(1)试用代数式表示出这个三位数.
(2)试写出所有符合条件的三位数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com