
【题目】如图,矩形ABCD中,AB=m,AD=n.
(1)若m=4,矩形ABCD的边CD上是否存在点P,使得∠APB=90°?写出点P存在或不存在的可能情况和此时n满足的条件.
(2)矩形ABCD的边上是否存在点P,使得∠APB=60°?写出点P存在或不存在的可能情况和此时m、n满足的条件.


【答案】(1)①当0<n<2时,CD上存在2个点P,使得∠APB=90°;②当n=2时,CD上存在1个点P,使得∠APB=90°;③当n>2时,CD上不存在满足条件的点P;(2)详见解析.
【解析】
(1)根据直角的定义与矩形的关系作图即可分析;
(2)根据含30°的直角三角形的性质结合图形即可求解.
(1)①如图,当0<n<2时,CD上存在2个点P,使得∠APB=90°;
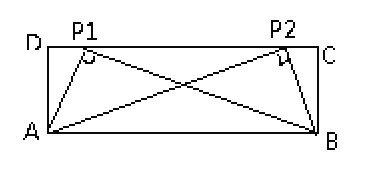
②如图当n=2时,CD上存在1个点P,使得∠APB=90°;
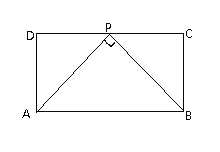
③如图当n>2时,CD上不存在满足条件的点P.
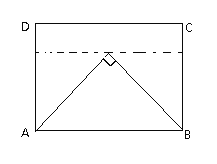
(2)①如图,当![]() =tan60°=
=tan60°=![]() 时,n=
时,n=![]() m时,矩形ABCD的边上存在2个点P,使得∠APB=60°;
m时,矩形ABCD的边上存在2个点P,使得∠APB=60°;
②故当n<![]() m时,矩形ABCD的边上不存在点P,使得∠APB=60°;
m时,矩形ABCD的边上不存在点P,使得∠APB=60°;
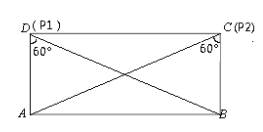
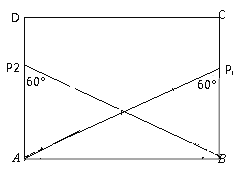
③如图,当△ABP为等边三角形时,当![]() =tan60°=
=tan60°=![]() ,即n=
,即n=![]() m时,矩形ABCD的边上存在3个点P,使得∠APB=60°;
m时,矩形ABCD的边上存在3个点P,使得∠APB=60°;
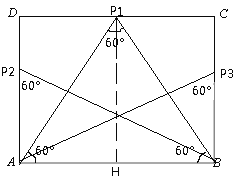
④如图,故当![]() m<n<
m<n<![]() m时,矩形ABCD的边上存在4个点P,使得∠APB=60°;
m时,矩形ABCD的边上存在4个点P,使得∠APB=60°;
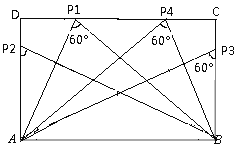
⑤如图,当n>![]() m时,矩形ABCD的边上存在2个点P,使得∠APB=60°.
m时,矩形ABCD的边上存在2个点P,使得∠APB=60°.


科目:初中数学 来源: 题型:
【题目】(1)如图(1),△ABC和△AOD都是等腰直角三角形,∠BAC=∠EAD=90°,点B在线段AE上,点C在线段AD上,请直接写出线段BE与线段CD的数量关系与位置关系;
(2)如图(2),将图(1)中的△ABC绕点A顺时针施转α(0°<α<360°),那么(1)中线段BE与线段CD的关系是否还成立?如果成立,请你结合图(2)给出的情形进行证明;如果不成立,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,直径
中,直径![]() 垂直弦
垂直弦![]() 于点
于点![]() ,且
,且![]() .点
.点![]() 为
为![]() 上一点(点
上一点(点![]() 不与点
不与点![]() ,
,![]() 重合),连结
重合),连结![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .过点
.过点![]() 作
作![]() 于点
于点![]() .给出下列结论:①
.给出下列结论:①![]() 是等边三角形;②在点
是等边三角形;②在点![]() 从
从![]() 的运动过程中,
的运动过程中,![]() 的值始终等于
的值始终等于![]() .则下列说法正确的是( )
.则下列说法正确的是( )
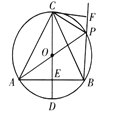
A.①,②都对B.①对,②错C.①错,②对D.①,②都错
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中,装有2个白球和1个红球,这些球除颜色外都相同.
(1)小明认为,搅匀后从中任意摸出一个球,不是白球就是红球是等可能的,你同意他的说法吗?为什么?
(2)搅匀后从中一把摸出两个球,请通过列表和树状图求出两个球都是白球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某排球队6名场上队员的身高(单位:cm)是:180,182,184,186,190,194.现用一名身高为188cm的队员换下场上身高为182cm的队员,与换人前相比,场上队员的身高
A.平均数变小,方差变小B.平均数变小,方差变大
C.平均数变大,方差变小D.平均数变大,方差变大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AB是⊙O的直径,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,∠E=30°,AC=5.
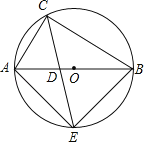
(1)求CE的长;
(2)求S△ADC:S△ACE的比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某小区有甲、乙两座楼房,楼间距BC为50米,在乙楼顶部A点测得甲楼顶部D点的仰角为37°,在乙楼底部B点测得甲楼顶部D点的仰角为60°,则甲、乙两楼的高度分别为多少?(结果精确到1米,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,我们规定:一个锐角的对边与斜边的比值称为这个锐角的正弦值.
例如:Rt△ABC中,∠C=90°,∠A的对边BC与斜边AB的比值,即![]() 就是∠A的正弦值.利用量角器可以制作“锐角正弦值速查卡”.制作方法如下:
就是∠A的正弦值.利用量角器可以制作“锐角正弦值速查卡”.制作方法如下:
如图,设OA=1,以O为圆心,分别以0.05,0.1,0.15,0.2,…,0.9,0.95长为半径作半圆,再以OA为直径作⊙M.利用“锐角正弦值速查卡”可以读出相应锐角正弦的近似值.例如:60°的正弦值约在0.85~0.88之间取值,45°的正弦值约在0.70~0.72之间取值.下列角度中正弦值最接近0.94的是( )
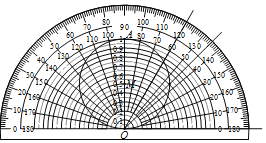
A.30°B.50°C.40°D.70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y1=﹣x+4,y2=![]() x+b都与双曲线y=
x+b都与双曲线y=![]() 交于点A(1,m),这两条直线分别与x轴交于B,C两点.
交于点A(1,m),这两条直线分别与x轴交于B,C两点.
(1)求y与x之间的函数关系式;
(2)直接写出当x>0时,不等式![]() x+b>
x+b>![]() 的解集;
的解集;
(3)若点P在x轴上,连接AP把△ABC的面积分成1:3两部分,求此时点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com