
【题目】在矩形ABCD中,AB=4,AD=6,M是AD边的中点,P是射线AB上的一个动点(不与A,B重合),MN⊥PM交射线BC于N点.
(1)如图1,当点N与点C重合时,求AP的长;
(2)如图2,在点N的运动过程中,求证: ![]() 为定值;
为定值;
(3)在射线AB上,是否存在点P,使得△DCN∽△PMN?若存在,求此时AP的长;若不存在,请说明理由.
【答案】
(1)
解:∵矩形ABCD,∴∠A=∠D=90°,
∵MN⊥PM,
∴∠APM=90°﹣∠AMP=∠DMC,
∴△APM∽△DMC,
∴ ![]() =
= ![]() ,
,
∵点M是AD的中点,
∴MD=AM= ![]() AD=3,
AD=3,
∵CD=AB=4,
∴ ![]() =
= ![]() ,
,
∴AP= ![]()
(2)
解:证明:①当点P在线段AB上时,如图2,

延长MN交DC的延长线于G,
同(1)的方法得出,△APM∽△DMG,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() +
+ ![]() =
= ![]() +
+ ![]() ,
,
∵AD∥CN,
∴∠CNG=∠DMG=∠APM,
∵∠PAM=∠NCG=90°,
∴△APM∽△CNG,
∴ ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ;
;
②当点P在AB的延长线上时,如图,

同①的方法得出,△APM∽△DMH,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
同①的方法得出,△APM∽△CNH,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() =
= ![]() ;
;
即: ![]() 是定值
是定值
(3)
解:存在点P,使得△DCN∽△PMN,
解:由(2)知 ![]() =
= ![]() ,△DCN∽△PMN时,
,△DCN∽△PMN时,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴CN=4,
易得,△MDH∽△NCH,
∴ ![]() =
= ![]() . =
. = ![]() ,
,
∵CD=AB=4,
∴DH= ![]() ,CH=
,CH= ![]() ,
,
由(2)②知,△APM∽△MDH,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
P= ![]()
【解析】(1)先判断出∠APM=∠DMC即可得出△APM∽△DMC,即 ![]() =
= ![]() ,再求出AM=MD=3,CD=4代入即可;(2)分两种情况①判断出,△APM∽△DMG,和△APM∽△CNG用得出的比例式化简即可得出结论;②同①的方法即可得出结论;(3)先求出CN,再用△MDH∽△NCH求出DH,CH,最后用△APM∽△MDH即可求出结论.
,再求出AM=MD=3,CD=4代入即可;(2)分两种情况①判断出,△APM∽△DMG,和△APM∽△CNG用得出的比例式化简即可得出结论;②同①的方法即可得出结论;(3)先求出CN,再用△MDH∽△NCH求出DH,CH,最后用△APM∽△MDH即可求出结论.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,把矩形纸片ABCD沿对角线折叠,设重叠部分为△EBD,那么下列说法错误的是( )

A. △EBD是等腰三角形,EB=ED B. 折叠后∠ABE和∠C′BD一定相等
C. 折叠后得到的图形是轴对称图形 D. △EBA和△EDC′一定是全等三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个零件的形状如图所示,按规定这个零件中∠A和∠DBC都应为直角,工人师傅量出了这个零件各边尺寸,那么这个零件符合要求吗?求出四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的推理.
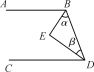
如图,BE平分∠ABD,DE平分∠BDC,且∠α+∠β=90°,试说明:AB∥CD.
完成推理过程:
∵BE平分∠ABD(已知),
∴∠ABD=2∠α(__________).
∵DE平分∠BDC(已知),
∴∠BDC=2∠β (__________).
∴∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β)( __________).
∵∠α+∠β=90°(已知),
∴∠ABD+∠BDC=180°(__________).
∴AB∥CD(____________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)求证:四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCF的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com