
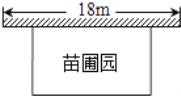
【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边由长为40米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃园的面积为102平方米,求x;
(2)若使这个苗圃园的面积最大,求出x和面积最大值.
【答案】(1)x=17;(2)当x=11米时,这个苗圃园的面积最大,最大值为198平方米.
【解析】
(1)根据题意列出方程,解出方程即可;
(2)设苗圃园的面积为y平方米,用x表达出y,得到二次函数表达式,根据二次函数的性质,求出面积的最大值,注意考虑是否符合实际情况.
(1)解:根据题意得:![]() ,
,
解得:![]() 或
或![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]()
(2)解:设苗圃园的面积为y平方米,则y=x(40﹣2x)=﹣2x2+40x =![]()
∵二次项系数为负,∴苗圃园的面积y有最大值.
∴当x=10时,即平行于墙的一边长是20米, 20>18,不符题意舍去;
∴当x=11时,y最大=198平方米;
答:当x=11米时,这个苗圃园的面积最大,最大值为198平方米.


科目:初中数学 来源: 题型:
【题目】我市某童装专卖店在销售中发现,一款童装每件进价为40元,若销售价为60元,每天可售出20件,为迎接“双十一”,专卖店决定采取适当的降价措施,以扩大销售量,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件![]() 设每件童装降价x元
设每件童装降价x元![]() 时,平均每天可盈利y元.
时,平均每天可盈利y元.
![]() 写出y与x的函数关系式;
写出y与x的函数关系式;
![]() 当该专卖店每件童装降价多少元时,平均每天盈利400元?
当该专卖店每件童装降价多少元时,平均每天盈利400元?
![]() 该专卖店要想平均每天盈利600元,可能吗?请说明理由.
该专卖店要想平均每天盈利600元,可能吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是圆O的直径,O为圆心,AD、BD是半圆的弦,且∠PDA=∠PBD.延长PD交圆的切线BE于点E
(1)证明:直线PD是⊙O的切线.
(2)如果∠BED=60°,![]() ,求PA的长.
,求PA的长.
(3)将线段PD以直线AD为对称轴作对称线段DF,点F正好在圆O上,如图2,求证:四边形DFBE为菱形.
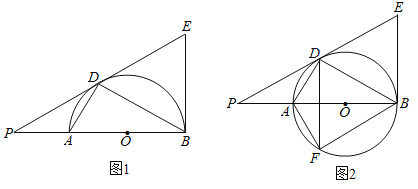
查看答案和解析>>
科目:初中数学 来源: 题型:
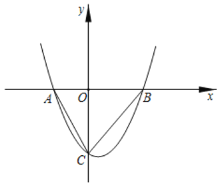
【题目】已知抛物线y=ax2+bx+c经过点A(﹣2,0),B(3,0),与y轴负半轴交于点C,且OC=OB.
(1)求抛物线的解析式;
(2)在y轴负半轴上存在一点D,使∠CBD=∠ADC,求点D的坐标;
(3)点D关于直线BC的对称点为D′,将抛物线y=ax2+bx+c向下平移h个单位,与线段DD′只有一个交点,直接写出h的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为建设最美恩施,一旅游投资公司拟定在某景区用茶花和月季打造一片人工花海,经市场调查,购买![]() 株茶花与
株茶花与![]() 株月季的费用相同,购买
株月季的费用相同,购买![]() 株茶花与
株茶花与![]() 株月季共需
株月季共需![]() 元.
元.
(1)求茶花和月季的销售单价;
(2)该景区至少需要茶花月季共![]() 株,要求茶花比月季多
株,要求茶花比月季多![]() 株,但订购两种花的总费用不超过
株,但订购两种花的总费用不超过![]() 元,该旅游投资公司怎样购买所需总费用最低,最低费用是多少.
元,该旅游投资公司怎样购买所需总费用最低,最低费用是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图的△ABC中,AB>AC>BC,且D为BC上一点。现打算在AB上找一点P,在AC上找一点Q,使得△APQ与以P、D、Q为顶点的三角形全等,以下是甲、乙两人的作法:
甲:连接AD,作AD的中垂线分别交AB、AC于P点、Q点,则P、Q两点即为所求;
乙:过D作与AC平行的直线交AB于P点,过D作与AB平行的直线交AC于Q点,则P、Q两点即为所求;
对于甲、乙两人的作法,下列判断何者正确( )?

A.两人皆正确B.两人皆错误C.甲正确,乙错误D.甲错误,乙正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为宣传6月6日世界海洋日,某校九年级举行了主题为“珍惜海洋资源,保护海洋生物多样性”的知识竞赛活动.为了解全年级500名学生此次竞赛成绩(百分制)的情况,随机抽取了部分参赛学生的成绩,整理并绘制出如下不完整的统计表(表1)和统计图(如图).请根据图表信息解答以下问题:
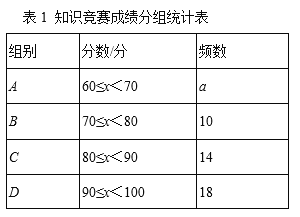

(1)本次调查一共随机抽取了_____个参赛学生的成绩;
(2)表1中a=_____;
(3)所抽取的参赛学生的成绩的中位数落在的“组别”是_____;
(4)请你估计,该校九年级竞赛成绩达到80分以上(含80分)的学生约有_____人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,二次函数y=ax2﹣3ax+c的图象与x轴交于点A、B,与y轴交于点c直线y=﹣x+4经过点B、C.
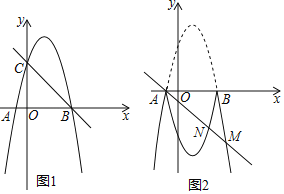
(1)求抛物线的表达式;
(2)过点A的直线y=kx+k交抛物线于点M,交直线BC于点N,连接AC,当直线y=kx+k平分△ABC的面积,求点M的坐标;
(3)如图2,把抛物线位于x轴上方的图象沿x轴翻折,当直线y=kx+k与翻折后的整个图象只有三个交点时,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)(1)问题发现
如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE,
填空:①∠AEB的度数为 ;
②线段AD、BE之间的数量关系是 .
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=900, 点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请判断∠AEB的度数及线段CM、AE、BE之间的数量关系,并说明理由.


(3)解决问题如图3,在正方形ABCD中,CD=![]() .若点P满足PD=1,且∠BPD=900,请直接写出点A到BP的距离.
.若点P满足PD=1,且∠BPD=900,请直接写出点A到BP的距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com