
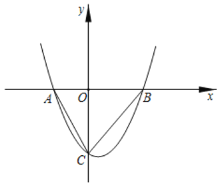
【题目】已知抛物线y=ax2+bx+c经过点A(﹣2,0),B(3,0),与y轴负半轴交于点C,且OC=OB.
(1)求抛物线的解析式;
(2)在y轴负半轴上存在一点D,使∠CBD=∠ADC,求点D的坐标;
(3)点D关于直线BC的对称点为D′,将抛物线y=ax2+bx+c向下平移h个单位,与线段DD′只有一个交点,直接写出h的取值范围.
【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣3;(2)D(0,﹣6);(3)3≤h≤15
x﹣3;(2)D(0,﹣6);(3)3≤h≤15
【解析】
(1)OC=OB,则点C(0,﹣3),抛物线的表达式为:y=a(x+2)(x﹣3)=a(x2﹣x﹣6),﹣6a=﹣3,解得:a=![]() ,即可求解;
,即可求解;
(2)CH=HD=![]() m,tan∠ADC=
m,tan∠ADC=![]() =tan∠DBC=
=tan∠DBC= ,解得:m=3或﹣4(舍去﹣4),即可求解;
,解得:m=3或﹣4(舍去﹣4),即可求解;
(3)过点C作x轴的平行线交DH的延长线于点D′,则D′(﹣3,﹣3);当平移后的抛物线过点C时,抛物线与线段DD′有一个公共点,此时,h=3;当平移后的抛物线过点D′时,抛物线与线段DD′有一个公共点,即可求解.
解:(1)OC=OB,则点C(0,﹣3),
抛物线的表达式为:y=a(x+2)(x﹣3)=a(x2﹣x﹣6),
﹣6a=﹣3,解得:a=![]() ,
,
故抛物线的表达式为:y=![]() x2﹣
x2﹣![]() x﹣3;
x﹣3;
(2)设CD=m,过点D作DH⊥BC交BC的延长线于点H,则CH=HD=![]() m,
m,
tan∠ADC=![]() =tan∠DBC=
=tan∠DBC= ,
,
解得:m=3或﹣4(舍去﹣4),
故点D(0,﹣6);
(3)过点C作x轴的平行线交DH的延长线于点D′,则D′(﹣3,﹣3);
平移后抛物线的表达式为:y=![]() x2﹣
x2﹣![]() x﹣3﹣h,
x﹣3﹣h,
当平移后的抛物线过点C时,抛物线与线段DD′有一个公共点,此时,h=3;
当平移后的抛物线过点D′时,抛物线与线段DD′有一个公共点,
即﹣3=![]() ×9+
×9+![]() ﹣h,解得:h=15,
﹣h,解得:h=15,
故3≤h≤15.



科目:初中数学 来源: 题型:
【题目】已知:正方形![]() 绕点
绕点![]() 顺时针旋转至正方形
顺时针旋转至正方形![]() ,连接
,连接![]() .
.
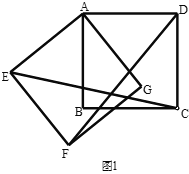
(1)如图,求证:![]() ;
;
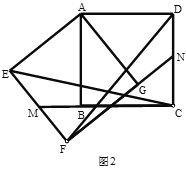
(2)如图,延长![]() 交
交![]() 于
于![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,在不添加任何辅助线的情况下,请直接写出如图中的四个角,使写出的每一个角的大小都等于旋转角.
,在不添加任何辅助线的情况下,请直接写出如图中的四个角,使写出的每一个角的大小都等于旋转角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在矩形ABCD中,点F是 BC的中点,DF的延长线与AB的延长线相交于点E,DE与AC相交于点O,若![]() ,则
,则![]() ( )
( )
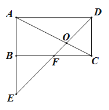
A. 4 B. 6 C. 8 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B在反比例函数![]() 的图象上,点C,D在反比例函数
的图象上,点C,D在反比例函数![]() 的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为
的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为![]() ,则k的值为( )
,则k的值为( )

A. 4 B. 3 C. 2 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】建设中的大外环路是我市的一项重点民生工程.某工程公司承建的一段路基工程的施工土方量为120万立方,原计划由公司的甲、乙两个工程队从公路的两端同时相向施工150天完成.由于特殊情况需要,公司抽调甲队外援施工,由乙队先单独施工40天后甲队返回,两队又共同施工了110天,这时甲乙两队共完成土方量103.2万立方.
(1)问甲、乙两队原计划平均每天的施工土方量分别为多少万立方?
(2)在抽调甲队外援施工的情况下,为了保证150天完成任务,公司为乙队新购进了一批机械来提高效率,那么乙队平均每天的施工土方量至少要比原来提高多少万立方才能保证按时完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是小明在健身器材上进行仰卧起坐锻炼时的情景,图②是小明锻炼时上半身由ON位置运动到与地面垂直的OM位置时的示意图.已知AC=0.66米,BD=0.26米,α=20°.(参考数据:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364)

(1)求AB的长(精确到0.01米);
(2)若测得ON=0.8米,试计算小明头顶由N点运动到M点的路径![]() 的长度.(结果保留π)
的长度.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
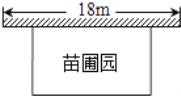
【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边由长为40米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃园的面积为102平方米,求x;
(2)若使这个苗圃园的面积最大,求出x和面积最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
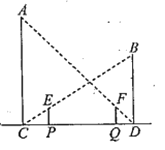
【题目】如图,王乐同学在晩上由路灯![]() 走向路灯
走向路灯![]() .当他行到
.当他行到![]() 处时发现,他往路灯
处时发现,他往路灯![]() 下的影长为2m,且恰好位于路灯
下的影长为2m,且恰好位于路灯![]() 的正下方,接着他又走了
的正下方,接着他又走了![]() 到
到![]() 处,此时他在路灯
处,此时他在路灯![]() 下的影孑恰好位于路灯
下的影孑恰好位于路灯![]() 的正下方(已知王乐身高
的正下方(已知王乐身高![]() ,路灯
,路灯![]() 高
高![]() ).
).
(1)王乐站在![]() 处时,在路灯
处时,在路灯![]() 下的影子是哪条线段?
下的影子是哪条线段?
(2)计算王乐站在![]() 处时,在路灯
处时,在路灯![]() 下的影长;
下的影长;
(3)计算路灯![]() 的高度.
的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】交通工程学理论把在单向道路上行驶的汽车看成连续的流体,并用流量、速度、密度三个概念描述车流的基本特征,其中流量![]() (辆
(辆![]() 小时)指单位时间内通过道路指定断面的车辆数;速度
小时)指单位时间内通过道路指定断面的车辆数;速度![]() (千米
(千米![]() 小时)指通过道路指定断面的车辆速度,密度
小时)指通过道路指定断面的车辆速度,密度![]() (辆
(辆![]() 千米)指通过道路指定断面单位长度内的车辆数.为配合大数据治堵行动,测得某路段流量
千米)指通过道路指定断面单位长度内的车辆数.为配合大数据治堵行动,测得某路段流量![]() 与速度
与速度![]() 之间关系的部分数据如下表:
之间关系的部分数据如下表:
速度v(千米/小时) |
|
|
|
|
|
|
|
|
流量q(辆/小时) |
|
|
|
|
|
|
|
|
(1)根据上表信息,下列三个函数关系式中,刻画![]() ,
,![]() 关系最准确是_____________________.(只填上正确答案的序号)
关系最准确是_____________________.(只填上正确答案的序号)
①![]() ;②
;②![]() ;③
;③![]()
(2)请利用(1)中选取的函数关系式分析,当该路段的车流速度为多少时,流量达到最大?最大流量是多少?
(3)已知![]() ,
,![]() ,
,![]() 满足
满足![]() ,请结合(1)中选取的函数关系式继续解决下列问题:市交通运行监控平台显示,当
,请结合(1)中选取的函数关系式继续解决下列问题:市交通运行监控平台显示,当![]() 时道路出现轻度拥堵.试分析当车流密度
时道路出现轻度拥堵.试分析当车流密度![]() 在什么范围时,该路段将出现轻度拥堵?
在什么范围时,该路段将出现轻度拥堵?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com