
分析 (1)用1cm表示10海里,根据题意画出图形即可;
(2)量出BC=3cm,推算出BC的实际距离,然后解直角三角形求得CD的实际距离;
(3)根据CD 的长度即可确定轮船到达D处时的时间.
解答 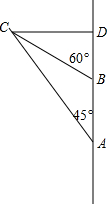 解:(1)用1cm表示10海里,如图所示;
解:(1)用1cm表示10海里,如图所示;
(2)量得BC=3cm,
∵AB=15×2=30(海里),∠CAB=45°,∠CBD=60°,
∴CD=AD,BD=$\frac{CD}{tan60°}$=$\frac{CD}{\sqrt{3}}$,
∵AB=AD-BD=CD-$\frac{CD}{\sqrt{3}}$=30,
∴CD=15(3+$\sqrt{3}$)海里.
答:CD的实际距离为15(3+$\sqrt{3}$)海里;
(3)能,
∵BD=$\frac{CD}{tan60°}$=15($\sqrt{3}+$1),
∴15($\sqrt{3}+$1)÷15=($\sqrt{3}+$1)≈2.7小时,
∴轮船到达D处时的时间12时42分.
点评 本题考查了解直角三角形的应用-方向角问题,等腰三角形的性质和判定,三角形的外角性质,关键是准确画出图形,求出∠C=∠CAB,题目比较典型,难度不大.


科目:初中数学 来源:2017届云南省普洱市九年级学业水平测试模拟考试(一)数学试卷(解析版) 题型:判断题
在形状、大小、质量完全相同且不透明的四张卡片中,分别写有数2、3、5、6,随机抽取一张卡片记下数字后放回,洗匀后,再抽取一张卡片记下数字.
(1)请用列表或树状图的方法表示可能出现的所有结果;
(2)设第一次取出的数字记为 ,第二次取出的数字记为
,第二次取出的数字记为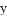 ,求两次抽到数字组成的点(x,y)在直线
,求两次抽到数字组成的点(x,y)在直线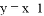 上的概率。
上的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
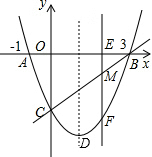 如图,抛物线与x轴交于点A(-1,0)、点B(3,0),交y轴于点C(0,-3),点M为线段BC上一动点,过点M作x轴的垂线,交x轴于点E,交抛物线于点F
如图,抛物线与x轴交于点A(-1,0)、点B(3,0),交y轴于点C(0,-3),点M为线段BC上一动点,过点M作x轴的垂线,交x轴于点E,交抛物线于点F查看答案和解析>>
科目:初中数学 来源: 题型:解答题
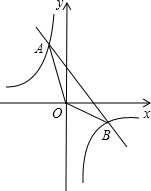 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(-1,3),B(3,a)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(-1,3),B(3,a)两点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
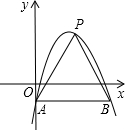 如图,在平面直角坐标系中,抛物线y=-(x-2)2+3与y轴交于点A,过点A与x轴平行的直线交抛物线于另一点B.点P是直线AB上方的抛物线上一点,设点P的横坐标为m,则△PAB的面积S的取值范围为0<S≤8.
如图,在平面直角坐标系中,抛物线y=-(x-2)2+3与y轴交于点A,过点A与x轴平行的直线交抛物线于另一点B.点P是直线AB上方的抛物线上一点,设点P的横坐标为m,则△PAB的面积S的取值范围为0<S≤8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com