【题目】如图，锐角
，
是
边上异于
、
的一点，过点作直线截，所截得的三角形与原相似，满足这样条件的直线共有（ ）条．
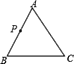
A. 1B. 2C. 3D. 4
【答案】D
【解析】
本题可以分两种方法，第一种：利用平行于三角形一边的直线和其他两边相交，所截得的三角形与原三角形相似的判定定理，过点P分别做AC与BC的平行线.第二种：利用两边对应成相等比例且夹角相等的两个三角形相似的判定定理，过P分别做PE交AC或交BC于点E，使使AE：AB=AP：AC或使BP：CB=BE：AB，夹角是公共角∠A或∠B.
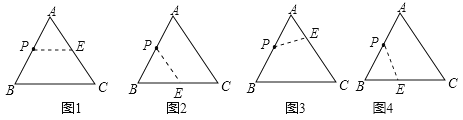
（1）如图1，作PE平行于BC，则△APE
△ABC,（2）如图2，作PE平行于AC，则△BPE△BAC,（3）如图3，作PE，使AE：AB=AP：AC,此时∠A.是公共角，△APE△ACB,（4）如图4，作PE，使BP：CB=BE：AB．此时∠B是公共角，△PEB△ACB
所以共有四种画法，即四条直线满足条件，故选D．
亮点激活精编提优100分大试卷系列答案科目：初中数学 来源： 题型：
【题目】在下表中，我们把第i行第j列的数记为
（其中i，j都是不大于5的正整数），对于表中的每个数，规定如下：当i≥j时，=l；当i<j时，=0。例如：当i=2，j=1时，=
=1。按此规定，
=______；表中的25个数中，共有_______个1；计算
+
·
+·
+
·
+
·
的值为_______。
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，点A，C分别在x轴、y轴上，四边形ABCO是边长为4的正方形，点D为AB的中点，点P为OB上的一个动点，连接DP，AP，当点P满足DP+AP的值最小时，直线AP的解析式为_____．
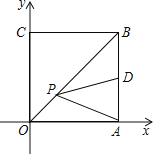
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】“低碳生活，绿色出行”,2017年1月,某公司向深圳市场新投放共享单车640辆.
（1）若1月份到4月份新投放单车数量的月平均增长率相同，3月份新投放共享单车1000辆.请问该公司4月份在深圳市新投放共享单车多少辆？
（2）考虑到自行车市场需求不断增加,某商城准备用不超过70000元的资金再购进A，B两种规格的自行车100辆，已知A型的进价为500元/辆，售价为700元/辆，B型车进价为1000元/辆，售价为1300元/辆。假设所进车辆全部售完，为了使利润最大，该商城应如何进货？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知⊙O中，AC为直径，MA、MB分别切⊙O于点A、B．
（1）如图①，若∠BAC=23°，求∠AMB的大小；
（Ⅱ）如图②，过点B作BD∥MA，交AC于点E，交⊙O于点D，若BD=MA，求∠AMB的大小．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，小明画了一个锐角
，并作出了它的两条高
和
，两高相交于点
．小明说图形中共有两对相似三角形，他说的对吗？请你判定一下，如果正确，就其中的一对进行说理．
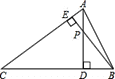
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，要把破残的圆片复制完整，已知弧上三点A、B、C.
(1)用尺规作图法，找出弧BAC所在圆的圆心O；(保留作图痕迹，不写作法)
(2)设△ABC为等腰三角形，底边BC=10 cm，腰AB=6 cm，求圆片的半径R；(结果保留根号)
(3)若在(2)题中的R满足n＜R＜m(m、n为正整数)，试估算m和n的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
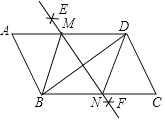
【题目】如图，BD是ABCD的对角线，按以下步骤作图：①分别以点B和点D为圆心，大于
BD的长为半径作弧，两弧相交于E，F两点；②作直线EF，分别交AD，BC于点M，N，连接BM，DN．若BD＝8，MN＝6，则ABCD的边BC上的高为___．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】抛物线
上部分点的横坐标
，纵坐标
的对应值如下表：
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
小聪观察上表，得出下面结论：①抛物线与x轴的一个交点为（3，0）； ②函数的最大值为6；③抛物线的对称轴是
；④在对称轴左侧，y随x增大而增大．其中正确有( )
A. ①② B. ①③ C. ①②③ D. ①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
