
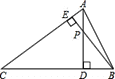
【题目】如图,小明画了一个锐角![]() ,并作出了它的两条高
,并作出了它的两条高![]() 和
和![]() ,两高相交于点
,两高相交于点![]() .小明说图形中共有两对相似三角形,他说的对吗?请你判定一下,如果正确,就其中的一对进行说理.
.小明说图形中共有两对相似三角形,他说的对吗?请你判定一下,如果正确,就其中的一对进行说理.
【答案】见解析
【解析】
由图可知,在直角△ADC中有一个小直角△AEP,它们公共角是∠CAD,另外都有一个直角,所以运用两个角对应相等的三角形相似可得△AEP∽△ADC,在直角△BCE中有一个小直角△BDP,同理得到△BDP∽△BEC.又直角△AEP与直角△BDP,有一个对顶角相等,且都有一个直角,所以△BDP∽△AEP.
则由三角形相似的传递性可知△AEP∽△ADC∽△BDP∽△BEC,则它们两两相似,故有六对.
小明的说法不正确,因为图形中存在着6对相似三角形. 它们分别是:△AEP∽△ADC,△AEP∽△BDP,△AEP∽△BEC,△ADC∽△BDP,△ADC∽△BEC,
△BDP∽△BEC
证明:∵BE⊥AC,AD⊥BC(已知)
∴∠CEP=∠AEP=90°
又∵∠CAD=∠PAE(公共角)
∴△AEP∽△ADC(两组角对应相等的两个三角形相似)
同理可得:△BDP∽△BEC
在△BDP与△AEP中
有∠AEP=∠BDP=90°
∠APE=∠BPD(对顶角相等)
∴△BDP∽△AEP(两组角对应相等的两个三角形相似)
由相似的传递性证得:△AEP∽△ADC∽△BDP∽△BEC
故有三角形两两相似六对:
△AEP∽△ADC,△AEP∽△BDP,△AEP∽△BEC,△ADC∽△BDP,△ADC∽△BEC,
△BDP∽△BEC


科目:初中数学 来源: 题型:
【题目】(1)如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE。
①∠AEB的度数为__________;
②线段AD,BE之间的数量关系为__________;
(2)如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并证明你的结论;
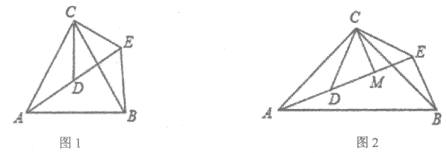
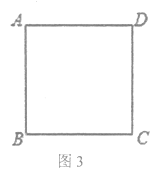
(3)如图3,在正方形ABCD中,CD=![]() ,若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离为________________________________。
,若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离为________________________________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两同学的家与某科技馆的距离均为4000m.甲、乙两人同时从家出发去科技馆,甲同学先步行800m,然后乘公交车,乙同学骑自行车.已知乙骑自行车的速度是甲步行速度的4倍,公交车的速度是乙骑自行车速度的2倍,结果甲同学比乙同学晚到2.5min.求乙到达科技馆时,甲离科技馆还有多远.
查看答案和解析>>
科目:初中数学 来源: 题型:
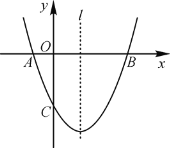
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-1,0),B(3,0),C(0,-3)三点,直线l是抛物线的对称轴.
(1)求抛物线的函数解析式;
(2)设点M是直线l上的一个动点,当点M到点A,点C的距离之和最短时,求点M的坐标;
(3)在抛物线上是否存在点N,使S⊿ABN=![]() S⊿ABC,若存在,求出点N的坐标,若不存在,说明理由.
S⊿ABC,若存在,求出点N的坐标,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点G,H分别是正六边形ABCDEF的边BC,CD上的点,且BG=CH,AG交BH于点P.
(1)求证:△ABG≌△BCH;
(2)求∠APH的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=k1x+b的图象与x轴、y轴分别交于A,B两点,与反比例函数y=![]() 的图象分别交于C,D两点,点C(2,4),点B是线段AC的中点.
的图象分别交于C,D两点,点C(2,4),点B是线段AC的中点.

(1)求一次函数y=k1x+b与反比例函数y=![]() 的解析式;
的解析式;
(2)求△COD的面积;
(3)直接写出当x取什么值时,k1x+b<![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
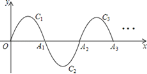
【题目】如图,一段抛物线:![]() (0≤x≤2)记为C1,它与x轴交于两点O、A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,直至得到C7,若点P(13,m)在第7段抛物线C7上,则m=_____.
(0≤x≤2)记为C1,它与x轴交于两点O、A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,直至得到C7,若点P(13,m)在第7段抛物线C7上,则m=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com