
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-1,0),B(3,0),C(0,-3)三点,直线l是抛物线的对称轴.
(1)求抛物线的函数解析式;
(2)设点M是直线l上的一个动点,当点M到点A,点C的距离之和最短时,求点M的坐标;
(3)在抛物线上是否存在点N,使S⊿ABN=![]() S⊿ABC,若存在,求出点N的坐标,若不存在,说明理由.
S⊿ABC,若存在,求出点N的坐标,若不存在,说明理由.
【答案】(1)y=x2-2x-3;(2) M(1,-2);(3) ![]() ,(1,-4).
,(1,-4).
【解析】
(1)直接将A、B、C三点坐标代入抛物线的解析式中求出待定系数即可;
(2)由图知:A、B点关于抛物线的对称轴对称,连接BC得出M点位置,即为符合条件的M点;
(3)根据题意可知OC=3,要使S⊿ABN=![]() S⊿ABC,则三角形ABN的高为4,即N点的纵坐标为±4,设点N的坐标为(x,±4),代入函数解析式求解即可得出N点的坐标.
S⊿ABC,则三角形ABN的高为4,即N点的纵坐标为±4,设点N的坐标为(x,±4),代入函数解析式求解即可得出N点的坐标.
解:(1)将A(-1,0)、B(3,0)、C(0,-3)代入抛物线y=ax2+bx+c中,得: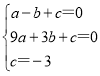
解得: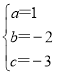
故抛物线的解析式:y=x2-2x-3.
(2)如图所示:连接BC,交直线l于点M,此时点M到点A,点C的距离之和最短,
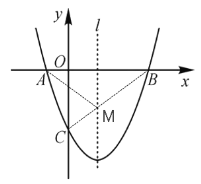
设直线BC的解析式为:y=kx+d,则![]()
解得:![]()
故直线BC的解析式为:y=x-3,
∵x=-![]() =1,
=1,
∴x=1时,y=1-3=-2,
故M(1,-2);
(3)存在,理由如下:
![]() 点C(0,-3),
点C(0,-3),
∴OC=3,即三角形ABC的高为3
要使S⊿ABN=![]() S⊿ABC,则三角形ABN的高为4,即N点的纵坐标为±4,
S⊿ABC,则三角形ABN的高为4,即N点的纵坐标为±4,
设N为(x,±4)
所以当y=4时,有x2-2x-3=4即x2-2x-7=0,解得![]()
当y=-4时,有x2-2x-3=-4即x2-2x+1=0,解得x=1
所以N点的坐标为![]() ,(1,-4)
,(1,-4)


科目:初中数学 来源: 题型:
【题目】改革开放40年以来,城乡居民生活水平持续快速提升。居民教育、文化和娱乐消费支出持续增长。下图为北京市统计局发布的2017年和2018年我市居民人均教育、文化和娱乐消费支出的折线图。
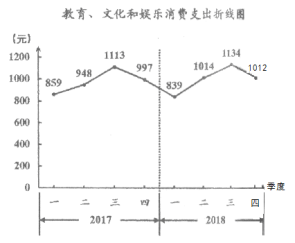
说明:在统计学中,同比是指本期统计数据与上一年同期统计数据相比较,例如2018年第二季度与2017年第二季度相比较;环比是指本期统计数据与上期统计数据相比较,例如2018年第二季度与2018年第一季度相比较。根据上述信息,下列结论中错误的是( )
A. 2017年第二季度环比有所提高
B. 2017年第四季度环比有所降低
C. 2018年第一季度同比有所提高
D. 2018年第四季度同比有所提高
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=﹣![]() x2+bx+c与x轴交于B,C两点,与y轴交于点A,直线y=﹣
x2+bx+c与x轴交于B,C两点,与y轴交于点A,直线y=﹣![]() x+2经过A,C两点,抛物线的对称轴与x轴交于点D,直线MN与对称轴交于点G,与抛物线交于M,N两点(点N在对称轴右侧),且MN∥x轴,MN=7.
x+2经过A,C两点,抛物线的对称轴与x轴交于点D,直线MN与对称轴交于点G,与抛物线交于M,N两点(点N在对称轴右侧),且MN∥x轴,MN=7.
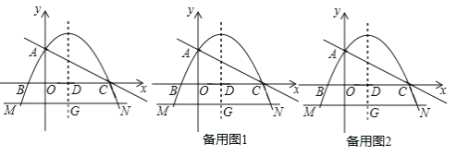
(1)求此抛物线的解析式.
(2)求点N的坐标.
(3)过点A的直线与抛物线交于点F,当tan∠FAC=![]() 时,求点F的坐标.
时,求点F的坐标.
(4)过点D作直线AC的垂线,交AC于点H,交y轴于点K,连接CN,△AHK沿射线AC以每秒1个单位长度的速度移动,移动过程中△AHK与四边形DGNC产生重叠,设重叠面积为S,移动时间为t(0≤t≤![]() ),请直接写出S与t的函数关系式.
),请直接写出S与t的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳生活,绿色出行”,2017年1月,某公司向深圳市场新投放共享单车640辆.
(1)若1月份到4月份新投放单车数量的月平均增长率相同,3月份新投放共享单车1000辆.请问该公司4月份在深圳市新投放共享单车多少辆?
(2)考虑到自行车市场需求不断增加,某商城准备用不超过70000元的资金再购进A,B两种规格的自行车100辆,已知A型的进价为500元/辆,售价为700元/辆,B型车进价为1000元/辆,售价为1300元/辆。假设所进车辆全部售完,为了使利润最大,该商城应如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分7分) 已知:如图,A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,AC=![]() OB.
OB.
(1)求证:AB是⊙O的切线;
(2)若∠ACD=45°,OC=2,求弦CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明画了一个锐角![]() ,并作出了它的两条高
,并作出了它的两条高![]() 和
和![]() ,两高相交于点
,两高相交于点![]() .小明说图形中共有两对相似三角形,他说的对吗?请你判定一下,如果正确,就其中的一对进行说理.
.小明说图形中共有两对相似三角形,他说的对吗?请你判定一下,如果正确,就其中的一对进行说理.
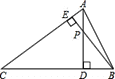
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 抛物线![]() 与
与![]() 交于点A
交于点A![]() ,过点A作
,过点A作![]() 轴的平行线,分别交两条抛物线于点B、C.则以下结论:① 无论
轴的平行线,分别交两条抛物线于点B、C.则以下结论:① 无论![]() 取何值,
取何值,![]() 的值总是正数;②
的值总是正数;② ![]() ;③ 当
;③ 当![]() 时,
时,![]() ;④ 当
;④ 当![]() >
>![]() 时,0≤
时,0≤![]() <1;⑤ 2AB=3AC.其中正确结论的编号是______________.
<1;⑤ 2AB=3AC.其中正确结论的编号是______________.
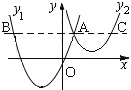
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°.点O是AB的中点,边AC=6,将边长足够大的三角板的直角顶点放在点O处,将三角板绕点0旋转,始终保持三角板的直角边与AC相交,交点为点E,另条直角边与BC相交,交点为D,则等腰直角三角板的直角边被三角板覆盖部分的两条线段CD与CE的长度之和为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com