
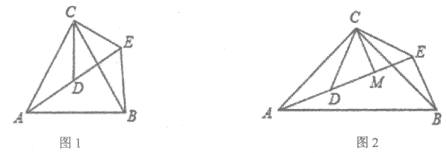
����Ŀ����1����ͼ1����ACB�͡�DCE��Ϊ�ȱ������Σ���A��D��E��ͬһֱ���ϣ�����BE��
�١�AEB�Ķ���Ϊ__________��
���߶�AD��BE֮���������ϵΪ__________��
��2����ͼ2����ACB�͡�DCE��Ϊ����ֱ�������Σ���ACB=��DCE=90������A��D��E��ͬһֱ���ϣ�CMΪ��DCE��DE���ϵĸߣ�����BE�����жϡ�AEB�Ķ������߶�CM��AE��BE֮���������ϵ����֤����Ľ��ۣ�
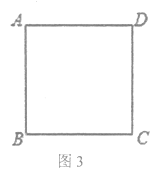
��3����ͼ3����������ABCD�У�CD=![]() ������P����PD=1���ҡ�BPD=90������ֱ��д����A��BP�ľ���Ϊ________________________________��
������P����PD=1���ҡ�BPD=90������ֱ��д����A��BP�ľ���Ϊ________________________________��
���𰸡���1����60������AD=BE����2����AEB=90����AE=BE+2CM�����ɼ���������3��A��BP�ľ���Ϊ![]() ��
��![]() .
.
��������
��1����������֤��ACD�ա�BCE���Ӷ��õ���AD=BE����ADC=��BEC���ɵ�A��D��E��ͬһֱ���Ͽ������ADC���Ӷ����������AEB�Ķ�����
��2�����գ�1���еĽⷨ�������AEB�Ķ�����֤��AD=BE������DCEΪ����ֱ�������μ�CMΪ��DCE��DE���ϵĸ߿ɵ�CM=DM=ME���Ӷ�֤��AE=2CH+BE��
��3����PD=1�ɵã���P���Ե�DΪԲ�ģ�1Ϊ�뾶��Բ�ϣ��ɡ�BPD=90���ɵã���P����BDΪֱ����Բ�ϣ���Ȼ����P��������Բ�Ľ��㣬������Բ���������㣬�������������λ�÷ֱ�������ۣ�Ȼ�������ʵ��ĸ����ߣ������ڣ�2���еĽ��ۼ��ɽ�����⣮
�⣺��1������ͼ1��
�ߡ�ACB����DCE��Ϊ�ȱ������Σ�
��CA=CB��CD=CE����ACB=��DCE=60����
���ACD=��BCE��
����ACD����BCE��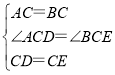
���ACD�ա�BCE��SAS����
���ADC=��BEC��
�ߡ�DCEΪ�ȱ������Σ�
���CDE=��CED=60����
�ߵ�A��D��E��ͬһֱ���ϣ�
���ADC=120����
���BEC=120����
���AEB=��BEC-��CED=60����
�ʴ�Ϊ��60����
�ڡߡ�ACD�ա�BCE��
��AD=BE��
�ʴ�Ϊ��AD=BE��
��2����AEB=90����AE=BE+2CM��
���ɣ���ͼ2��
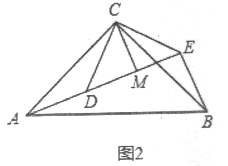
�ߡ�ACB����DCE��Ϊ����ֱ�������Σ�
��CA=CB��CD=CE����ACB=��DCE=90����
���ACD=��BCE��
����ACD����BCE��
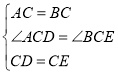
���ACD�ա�BCE��
��AD=BE����ADC=��BEC��
�ߡ�DCEΪ����ֱ�������Σ�
���CDE=��CED=45����
�ߵ�A��D��E��ͬһֱ���ϣ�
���ADC=135����
���BEC=135����
���AEB=��BEC����CED=90����
��CD=CE��CM��DE��
��DM=ME��
�ߡ�DCE=90����
��DM=ME=CM��
��AE=AD+DE=BE+2CM��
��3��A��BP�ľ���Ϊ![]() ��
��![]() ��
��
�������£�
��PD=1��
���P���Ե�DΪԲ�ģ�1Ϊ�뾶��Բ�ϣ�
�ߡ�BPD=90����
���P����BDΪֱ����Բ�ϣ�
���P������Բ�Ľ��㣮
�ٵ���P����ͼ3����ʾλ��ʱ��
����PD��PB��PA����AH��BP������ΪH��
����A��AE��AP����BP�ڵ�E����ͼ3�٣�
���ı���ABCD�������Σ�
���ADB=45����AB=AD=DC=BC=![]() ����BAD=90����
����BAD=90����
��BD=![]() ��
��
��DP=1��
��BP=![]() ��
��
�ߡ�BPD=��BAD=90����
��A��P��D��B����BDΪֱ����Բ�ϣ�
���APB=��ADB=45����
���PAE�ǵ���ֱ�������Σ�
�֡ߡ�BAD�ǵ���ֱ�������Σ���B��E��P���ߣ�AH��BP��
���ɣ�2���еĽ��ۿɵã�BP=2AH+PD��
��![]() =2AH+1��
=2AH+1��
��AH=![]() ��
��

�ڵ���P����ͼ3����ʾλ��ʱ��
����PD��PB��PA����AH��BP������ΪH��
����A��AE��AP����PB���ӳ����ڵ�E����ͼ3�ڣ�
ͬ���ɵã�BP=2AH-PD��
��![]() =2AH-1��
=2AH-1��
��AH=![]() ��
��
������������A��BP�ľ���Ϊ![]() ��
��![]() ��
��
�ʴ�Ϊ����1����60������AD=BE����2����AEB=90����AE=BE+2CM�����ɼ���������3��A��BP�ľ���Ϊ![]() ��
��![]() ��
��


 ����ʦ��Сһ����ʦ������ҵϵ�д�
����ʦ��Сһ����ʦ������ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
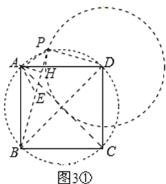
����Ŀ����ͼ����֪������![]() ������D��0��
������D��0��![]() ����ֱ���������߽��ڵ�M��N����
����ֱ���������߽��ڵ�M��N����![]() �ύ�ڵ�E���ҵ�M��N���ڵ�E�Գƣ���ֱ��MN�Ľ���ʽ��
�ύ�ڵ�E���ҵ�M��N���ڵ�E�Գƣ���ֱ��MN�Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ϵ�У���ֱ֪��y=-![]() x+4��y�ύ��A�㣬��x�ύ��B�㣬C������Ϊ����2��0����
x+4��y�ύ��A�㣬��x�ύ��B�㣬C������Ϊ����2��0����
��1����A��B��C����������ߵĽ���ʽ��
��2�����MΪ�����ߵĶ��㣬����AM��BM�����ı���AOBM�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ĸ↑��40�������������������ˮƽ������������������������Ļ�����������֧��������������ͼΪ������ͳ�ƾַ�����2017���2018�����о����˾��������Ļ�����������֧��������ͼ��
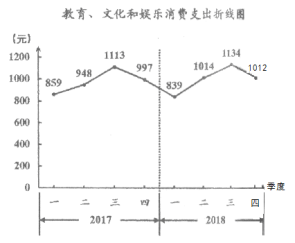
˵������ͳ��ѧ�У�ͬ����ָ����ͳ����������һ��ͬ��ͳ��������Ƚϣ�����2018��ڶ�������2017��ڶ�������Ƚϣ�������ָ����ͳ������������ͳ��������Ƚϣ�����2018��ڶ�������2018���һ������Ƚϡ�����������Ϣ�����н������������ǣ� ��
A. 2017��ڶ����Ȼ����������
B. 2017����ļ��Ȼ�����������
C. 2018���һ����ͬ���������
D. 2018����ļ���ͬ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����±��У����ǰѵ�i�е�j�е�����Ϊ![]() ������i��j���Dz�����5���������������ڱ��е�ÿ����
������i��j���Dz�����5���������������ڱ��е�ÿ����![]() ���涨���£���i��jʱ��
���涨���£���i��jʱ��![]() =l����i<jʱ��
=l����i<jʱ��![]() =0�����磺��i=2��j=1ʱ��
=0�����磺��i=2��j=1ʱ��![]() =
=![]() =1�����˹涨��
=1�����˹涨��![]() =______�����е�25�����У�����_______��1������
=______�����е�25�����У�����_______��1������![]() +
+![]() ��
��![]() +
+![]() ��
��![]() +
+![]() ��
��![]() +
+![]() ��
��![]() ��ֵΪ_______��
��ֵΪ_______��
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ1��ʾ������ɡ��ɡ����ֱ��ˮƽ���棬��ʾ��ͼ��ͼ2����ɡ�ս�ʱ����P���A�غϣ���ɡ�����ſ�ʱ������P��A��B�ƶ�������P�����Bʱ��ɡ�ŵ������֪ɡ�ڳſ��Ĺ����У�����PM=PN=CM=CN=6.0���ף�CE=CF=18.0���ף�BC=2.0���ף�
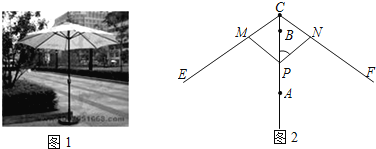
�v1�w��AP����ȡֵ��Χ��
�v2�w�����ⴹֱ�����£�ɡ�ŵ��ʱ����ɡ�µ���Ӱ�v�ٶ�ΪԲ��w���S�v����������w��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1������֪�ı���ABCD��һ��O�������ı���A��B��C��D����ʹ�����ı���ABCD���ڵ�O�Գƣ������O��������ͼ��2����ʾλ��,�ָ���ô��ͼ��?

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
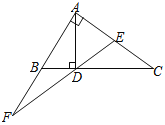
����Ŀ����֪����ͼ����Rt��ABC�У���BAC��90����AD��BC��D��EΪֱ�DZ�AC���е㣬��D��E��ֱ�߽�AB���ӳ�����F.��֤��![]() ��
��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
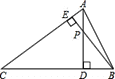
����Ŀ����ͼ��С������һ�����![]() ��������������������
��������������������![]() ��
��![]() �������ཻ�ڵ�
�������ཻ�ڵ�![]() ��С��˵ͼ���й����������������Σ���˵�Ķ��������ж�һ�£������ȷ�������е�һ�Խ���˵����
��С��˵ͼ���й����������������Σ���˵�Ķ��������ж�һ�£������ȷ�������е�һ�Խ���˵����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com