
����Ŀ��ͼ1��ʾ������ɡ��ɡ����ֱ��ˮƽ���棬��ʾ��ͼ��ͼ2����ɡ�ս�ʱ����P���A�غϣ���ɡ�����ſ�ʱ������P��A��B�ƶ�������P�����Bʱ��ɡ�ŵ������֪ɡ�ڳſ��Ĺ����У�����PM=PN=CM=CN=6.0���ף�CE=CF=18.0���ף�BC=2.0���ף�
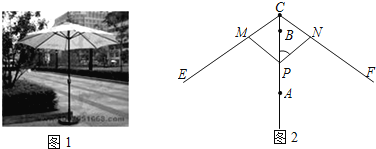
�v1�w��AP����ȡֵ��Χ��
�v2�w�����ⴹֱ�����£�ɡ�ŵ��ʱ����ɡ�µ���Ӱ�v�ٶ�ΪԲ��w���S�v����������w��
���𰸡���1��AP��ȡֵ��Χ�ǣ�0��x��10����2��S���=315����ƽ�����ף���
��������
��1���������⣬��AC=CN+PN����һ�����AB�ij����������AP��ȡֵ��Χ��
��2������MN��EF���ֱ�AC��B��H�������������CMPN���������MB�ij����ٸ������������εĶ�Ӧ�ߵı���ȣ����Բ�İ뾶�������ö��κ���������������ɣ�
��1����BC=2���ף�AC=CN+PN=12���ף�
��AB=AC��BC=10���ף�
����AP=x����AP��ȡֵ��Χ�ǣ�0��x��10��
��2������MN��EF���ֱ�AC��B��H��

��AP=x���ף�
��PM=PN=CM=CN��
���ı���PNCM�����Σ�
��MN��PC���ഹֱƽ�֣�AC�ǡ�ECF��ƽ���ߣ�
PB=![]()
��Rt��MBP�У�PM=6���ף�
��MB2=PM2��PB2=62����6��![]() x��2=6x��
x��2=6x��![]() x2��
x2��
��CE=CF��AC�ǡ�ECF��ƽ���ߣ�
��EH=HF��EF��AC��
�ߡ�ECH=��MCB����EHC=��MBC=90�㣬
���CMB�ס�CEH��
��![]() ��
��
��![]() =��
=��![]() ��2=
��2=![]()
��EH2=9MB2=9��6x��![]() x2����
x2����
��S=��EH2=9����6x��![]() x2����
x2����
��S=��![]() ��x2+54��x��
��x2+54��x��
��x=��![]() =12��0��x��10��
=12��0��x��10��
��x=10ʱ��S���=��![]() ����100+54����10=315����ƽ�����ף���
����100+54����10=315����ƽ�����ף���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
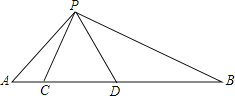
����Ŀ����ͼ����C��D���߶�AB�ϣ���PCD�ǵȱ������Σ�����ACP�ס�PDB��
��1������APB�Ĵ�С��
��2��˵���߶�AC��CD��BD֮���������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
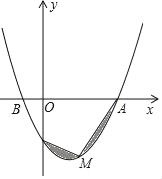
����Ŀ����ͼ����֪�����߹���A��4��0����B����2��0����C��0����4����
��1���������ߵĽ���ʽ��
��2����ͼ����M��������AC���ϵ�һ�����㣬��ͼ����Ӱ���ֵ������Сֵʱ�����M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1�����߶�AB����һ��C��C��AB��ΪAC��CB���Σ�����BC�ǽ�С��һ�Σ����BC��AB=AC2����ô���߶�AB����C�ƽ�ָ
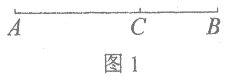
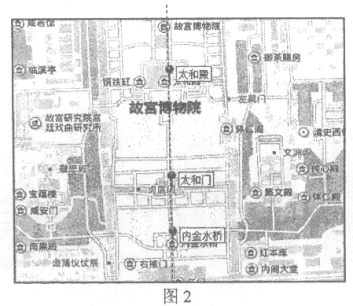
Ϊ���������У��ƽ�ָ����Ӧ���ڻ滭�����ܡ����֡�����������������ͼ2�����ҹ��Ŵ��Ͻ��ǵ��������ϣ�̫����λ��̫�͵����ڽ�ˮ��֮�俿���ڽ�ˮ�ŵ�һ�࣬����������λ�ù�ϵ����ƽ�ָ��֪̫�͵�ڽ�ˮ�ŵľ���ԼΪ100�ɣ���̫���ŵ�̫�͵�֮��ľ��루![]() �Ľ���ֵȡ2.2����
�Ľ���ֵȡ2.2����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ1����ACB�͡�DCE��Ϊ�ȱ������Σ���A��D��E��ͬһֱ���ϣ�����BE��
�١�AEB�Ķ���Ϊ__________��
���߶�AD��BE֮���������ϵΪ__________��
��2����ͼ2����ACB�͡�DCE��Ϊ����ֱ�������Σ���ACB=��DCE=90������A��D��E��ͬһֱ���ϣ�CMΪ��DCE��DE���ϵĸߣ�����BE�����жϡ�AEB�Ķ������߶�CM��AE��BE֮���������ϵ����֤����Ľ��ۣ�
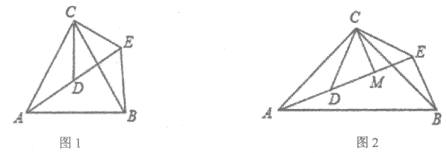
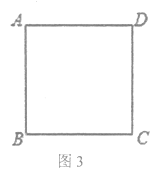
��3����ͼ3����������ABCD�У�CD=![]() ������P����PD=1���ҡ�BPD=90������ֱ��д����A��BP�ľ���Ϊ________________________________��
������P����PD=1���ҡ�BPD=90������ֱ��д����A��BP�ľ���Ϊ________________________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������Щ������ͼ�������������λ�����������������ת��֪ʶ��һ��ͼ���Ļ����ϼӹ����ɵģ�ÿһ��ͼ�������Կ���������������ͼ��������������ת������ת�����ģ���ת�ĽǶ���ȷ��Ϊ�� ��
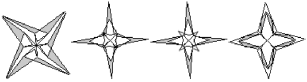
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
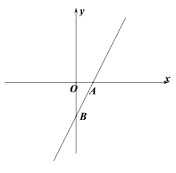
����Ŀ����ͼ��ֱ��AB��x�ύ�ڵ�A��1��0������y�ύ�ڵ�B��0��-2����
��1����ֱ��AB�Ľ���ʽ��
��2������C��ֱ��AB�ϣ���![]() �����C�����꣮
�����C�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
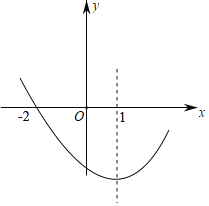
����Ŀ����ͼ�����κ���y��ax2+bx+c��a��0����ͼ����㣨��2��0�����Գ���Ϊֱ��x��1�������½��ۣ�
��abc��0��
��8a+c��0��
����A��x1��m����B��x2��m�����������ϵ����㣬��x��x1+x2ʱ��y��c��
�ܵ�M��N����������x����������㣬����x���·����������ϴ���һ��P��ʹ��PM��PN����a��ȡֵ��ΧΪa��1��
��������a��x+2����4��x������2������Ϊx1��x2����x1��x2����2��x1��x2��4��
���н�����ȷ���У�������
A. 2��B. 3��C. 4��D. 5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����G��H�ֱ�����������ABCDEF�ı�BC��CD�ϵĵ㣬��BG=CH��AG��BH�ڵ�P��
��1����֤����ABG�ա�BCH��
��2�����APH�Ķ�����

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com