
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§yЃНax2+bx+cЃЈaЁй0ЃЉЕФЭМЯѓЙ§ЕуЃЈЉ2ЃЌ0ЃЉЃЌЖдГЦжсЮЊжБЯпxЃН1ЃЎгавдЯТНсТлЃК
ЂйabcЃО0ЃЛ
Ђк8a+cЃО0ЃЛ
ЂлШєAЃЈx1ЃЌmЃЉЃЌBЃЈx2ЃЌmЃЉЪЧХзЮяЯпЩЯЕФСНЕуЃЌЕБxЃНx1+x2ЪБЃЌyЃНcЃЛ
ЂмЕуMЃЌNЪЧХзЮяЯпгыxжсЕФСНИіНЛЕуЃЌШєдкxжсЯТЗНЕФХзЮяЯпЩЯДцдквЛЕуPЃЌЪЙЕУPMЁЭPNЃЌдђaЕФШЁжЕЗЖЮЇЮЊaЁн1ЃЛ
ЂнШєЗНГЬaЃЈx+2ЃЉЃЈ4ЉxЃЉЃНЉ2ЕФСНИљЮЊx1ЃЌx2ЃЌЧвx1ЃМx2ЃЌдђЉ2Ёмx1ЃМx2ЃМ4ЃЎ
ЦфжаНсТле§ШЗЕФгаЃЈЁЁЁЁЃЉ
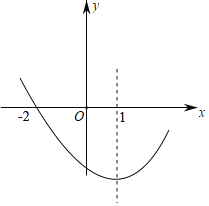
A. 2ИіB. 3ИіC. 4ИіD. 5Иі
ЁОД№АИЁПA
ЁОНтЮіЁП
ЂйгЩЭМЯѓПЩжЊaЃО0ЃЌcЃМ0ЃЌИљОнЖдГЦжс![]() ЃЌЕУЕНb<0ЃЌМДПЩХаЖЯЃЛ
ЃЌЕУЕНb<0ЃЌМДПЩХаЖЯЃЛ
ЂкгЩЖдГЦжс![]() ЕУЃЌbЃНЉ2aЃЌШЛКѓАбxЃНЉ2ДњШыНтЮіЪНЃЌећРэКѓМДПЩХаЖЯЃЛ
ЕУЃЌbЃНЉ2aЃЌШЛКѓАбxЃНЉ2ДњШыНтЮіЪНЃЌећРэКѓМДПЩХаЖЯЃЛ
ЂлИљОнХзЮяЯпЕФЖдГЦадЃЌЕУx1+x2=2ЃЌШЛКѓАбxЃН2ДњШыНтЮіЪНЃЌМДПЩХаЖЯЃЛ
ЂмгЩЕуMЃЌNЪЧХзЮяЯпгыxжсЕФСНИіНЛЕуЃЌдђХзЮяЯпЕФЖЅЕуЕНxжсЕФОрРыВЛаЁгк3ЃЌдђга![]() ЃЌНсКЯЂкЕФНсТлЃЌМДПЩЧѓЕУaЕФШЁжЕЗЖЮЇЃЛ
ЃЌНсКЯЂкЕФНсТлЃЌМДПЩЧѓЕУaЕФШЁжЕЗЖЮЇЃЛ
ЂнгЩЭМЯёПЩжЊЃЌгыxжсЕФСНИіНЛЕуЮЊЃЈ-2ЃЌ0ЃЉЃЌЃЈ4ЃЌ0ЃЉЃЌДЫЪБy=0ЃЌдђЕБy=2ЪБЃЌx1ЃМЉ2ЃМ4ЃМx2ЃЌМДПЩЕУЕНД№АИ.
НтЃКЂйгЩЭМЯѓПЩжЊЃКaЃО0ЃЌcЃМ0ЃЌ
![]()
ЁрabcЃО0ЃЌЙЪЂйе§ШЗЃЛ
ЂкЁпХзЮяЯпЕФЖдГЦжсЮЊжБЯпxЃН1ЃЌХзЮяЯпЕФЖдГЦжсЮЊжБЯпxЃН1ЃЌ
![]()
ЁрbЃНЉ2aЃЌ
ЕБxЃНЉ2ЪБЃЌyЃН4aЉ2b+cЃН0ЃЌ
Ёр4a+4a+cЃН0ЃЌ
Ёр8a+cЃН0ЃЌЙЪЂкДэЮѓЃЛ
ЂлЁпAЃЈx1ЃЌmЃЉЃЌBЃЈx2ЃЌmЃЉЪЧХзЮяЯпЩЯЕФСНЕуЃЌ
гЩХзЮяЯпЕФЖдГЦадПЩжЊЃКx1+x2ЃН1ЁС2ЃН2ЃЌ
ЁрЕБxЃН2ЪБЃЌyЃН4a+2b+cЃН4aЉ4a+cЃНcЃЌЙЪЂле§ШЗЃЛ
ЂмгЩЬтвтПЩжЊЃКMЃЌNЕНЖдГЦжсЕФОрРыЮЊ3ЃЌ
ЕБХзЮяЯпЕФЖЅЕуЕНxжсЕФОрРыВЛаЁгк3ЪБЃЌ
дкxжсЯТЗНЕФХзЮяЯпЩЯДцдкЕуPЃЌЪЙЕУPMЁЭPNЃЌ
МД![]() ЃЌ
ЃЌ
Ёп8a+cЃН0ЃЌ
ЁрcЃНЉ8aЃЌ
ЁпbЃНЉ2aЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌЙЪЂмДэЮѓЃЛ
ЃЌЙЪЂмДэЮѓЃЛ
ЂнвзжЊХзЮяЯпгыxжсЕФСэЭтвЛИіНЛЕузјБъЮЊЃЈ4ЃЌ0ЃЉЃЌ
ЁрyЃНax2+bx+cЃНaЃЈx+2ЃЉЃЈxЉ4ЃЉ
ШєЗНГЬaЃЈx+2ЃЉЃЈ4ЉxЃЉЃНЉ2ЃЌ
МДЗНГЬaЃЈx+2ЃЉЃЈxЉ4ЃЉЃН2ЕФСНИљЮЊx1ЃЌx2ЃЌ
дђx1ЁЂx2ЮЊХзЮяЯпгыжБЯпyЃН2ЕФСНИіНЛЕуЕФКсзјБъЃЌ
Ёпx1ЃМx2ЃЌ
Ёрx1ЃМЉ2ЃМ4ЃМx2ЃЌЙЪЂнДэЮѓЃЛ
ЙЪбЁЃКAЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОиаЮжНЦЌABCDжаЃЌABЃН3ЃЌBCЃН2ЃЌбиЖдНЧЯпACМєПЊЃЈШчЭМЂйЃЉЃЛЙЬЖЈЁїADCЃЌАбЁїABCбиADЗНЯђЦНвЦЃЈШчЭМЂкЃЉЃЌЕБСНИіШ§НЧаЮжиЕўВПЗжЕФУцЛ§зюДѓЪБЃЌвЦЖЏЕФОрРыAAЁфЕШгкЃЈ ЃЉ

A. 1 B. 1.5 C. 2 D. 0.8Лђ1.2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЕцЧђЪЧХХЧђЖгГЃЙцбЕСЗЕФживЊЯюФПжЎвЛЃЎЯТСаЭМБэжаЕФЪ§ОнЪЧМзЁЂввЁЂБћШ§ШЫУПШЫЪЎДЮЕцЧђВтЪдЕФГЩМЈЃЎВтЪдЙцдђЮЊУПДЮСЌајНгЧђ10ИіЃЌУПЕцЧђЕНЮЛ1ИіМЧ1ЗжЃЎ
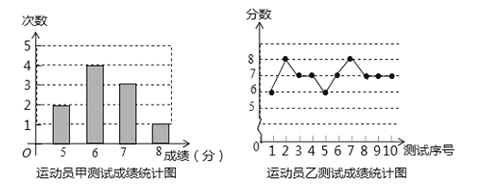
дЫЖЏдББћВтЪдГЩМЈЭГМЦБэ
ВтЪдађКХ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
ГЩМЈЃЈЗжЃЉ | 7 | 6 | 8 |
| 7 | 5 | 8 |
| 8 | 7 |
дЫЖЏдББћВтЪдГЩМЈЕФЦНОљЪ§КЭжкЪ§ЖМЪЧ7ЃЌ
ЃЈ1ЃЉГЩМЈБэжаЕФ![]() __________ЃЌ
__________ЃЌ![]() _________ЃЛ
_________ЃЛ
ЃЈ2ЃЉШєдкЫћУЧШ§ШЫжабЁдёвЛЮЛЕцЧђГЩМЈгХауЧвНЯЮЊЮШЖЈЕФНгЧђФмЪжзїЮЊздгЩШЫЃЌФуШЯЮЊбЁЫИќКЯЪЪЃПЧыгУФуЫљбЇЙ§ЕФЭГМЦСПМгвдЗжЮіЫЕУїЃЈВЮПМЪ§ОнЃКШ§ШЫГЩМЈЕФЗНВюЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЉ
ЃЉ
ЃЈ3ЃЉМзЁЂввЁЂБћШ§ШЫЯрЛЅжЎМфНјааЕцЧђСЗЯАЃЌУПИіШЫЕФЧђЖМЕШПЩФмЕФДЋИјЦфЫћСНШЫЃЌЧђДгввЪжжаДЋГіЃЌЧђДЋвЛДЮМзЕУЕНЧђЕФИХТЪЪЧ____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌвбжЊвЛДЮКЏЪ§![]() ЃЈkЁй0ЃЉЕФЭМЯѓгыxжсЁЂyжсЗжБ№НЛгкAЁЂBСНЕуЃЌЧвгыЗДБШР§КЏЪ§
ЃЈkЁй0ЃЉЕФЭМЯѓгыxжсЁЂyжсЗжБ№НЛгкAЁЂBСНЕуЃЌЧвгыЗДБШР§КЏЪ§![]() ЃЈmЁй0ЃЉЕФЭМЯѓдкЕквЛЯѓЯоНЛгкCЕуЃЌCDДЙжБгкxжсЃЌДЙзуЮЊDЃЎШєOA=OB=OD=1ЃЎ
ЃЈmЁй0ЃЉЕФЭМЯѓдкЕквЛЯѓЯоНЛгкCЕуЃЌCDДЙжБгкxжсЃЌДЙзуЮЊDЃЎШєOA=OB=OD=1ЃЎ
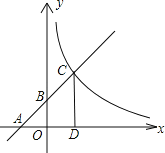
ЃЈ1ЃЉЧѓЕуAЁЂBЁЂDЕФзјБъЃЛ
ЃЈ2ЃЉЧѓвЛДЮКЏЪ§КЭЗДБШР§КЏЪ§ЕФНтЮіЪНЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЧыдФЖСЯТСаНтЬтЙ§ГЬЃК
НтвЛдЊЖўДЮВЛЕШЪНЃК![]() .
.
НтЃК![]()
![]() ЃЌЛђ
ЃЌЛђ![]() ЃЌ
ЃЌ
НтЕУ![]() Лђ
Лђ![]() .
.
![]() вЛдЊЖўДЮВЛЕШЪН
вЛдЊЖўДЮВЛЕШЪН![]() ЕФНтМЏЮЊ
ЕФНтМЏЮЊ![]() Лђ
Лђ![]() .
.
НсКЯЩЯЪіНтД№Й§ГЬЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЩЯЪіНтЬтЙ§ГЬЩјЭИЕФЪ§бЇЫМЯыЮЊ________ЃЛ
ЃЈ2ЃЉвЛдЊЖўДЮВЛЕШЪН![]() ЕФНтМЏЮЊ________ЃЛ
ЕФНтМЏЮЊ________ЃЛ
ЃЈ3ЃЉЧыгУРрЫЦЕФЗНЗЈНтвЛдЊЖўДЮВЛЕШЪНЃК![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫФБпаЮABCDжаЃЌЁЯBADЃНЁЯBCDЃН90ЁуЃЌЁЯABCЃН45ЁуЃЌСЌНгBDЃЌЕуOЮЊBDЕФжаЕуЃЌСЌНгAOВЂбгГЄНЛBCгкЕуEЃЌШє![]() ЃЌCDЃН4ЃЌдђADЕФГЄЮЊ_____ЃЎ
ЃЌCDЃН4ЃЌдђADЕФГЄЮЊ_____ЃЎ
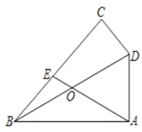
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
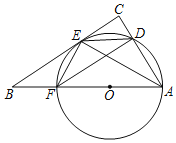
ЁОЬтФПЁПШчЭМЃЌAFЮЊЁбOЕФжБОЖЃЌЕуBдкAFЕФбгГЄЯпЩЯЃЌBEЧаЁбOгкЕуEЃЌЙ§ЕуAзїACЁЭBEЃЌНЛBEЕФбгГЄЯпНЛгкЕуCЃЌНЛЁбOНЛгкЕуDЃЌСЌНгAEЃЌEFЃЌFDЃЌDEЃЎ
ЃЈ1ЃЉЧѓжЄЃКEFЃНEDЃЎ
ЃЈ2ЃЉЧѓжЄЃКDFAFЃН2AEEFЃЎ
ЃЈ3ЃЉШєAEЃН4![]() ЃЌDEЃН2
ЃЌDEЃН2![]() ЃЌЧѓsinЁЯDFAЕФжЕЃЎ
ЃЌЧѓsinЁЯDFAЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
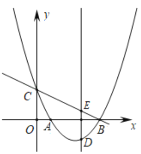
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() гы
гы![]() жсНЛгкСНЕу
жсНЛгкСНЕу![]() КЭ
КЭ![]() ЃЌгы
ЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌЕу
ЃЌЕу![]() ЪЧХзЮяЯпЩЯвЛИіЖЏЕуЃЌЙ§Еу
ЪЧХзЮяЯпЩЯвЛИіЖЏЕуЃЌЙ§Еу![]() зї
зї![]() жсЕФДЙЯпЃЌгыжБЯп
жсЕФДЙЯпЃЌгыжБЯп![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕБЕу![]() дкжБЯп
дкжБЯп![]() ЯТЗНЕФХзЮяЯпЩЯдЫЖЏЪБЃЌЯпЖЮ
ЯТЗНЕФХзЮяЯпЩЯдЫЖЏЪБЃЌЯпЖЮ![]() ЕФГЄЖШЪЧЗёДцдкзюДѓжЕЃПДцдкЕФЛАЃЌЧѓГіЦфзюДѓжЕКЭДЫЪБЕу
ЕФГЄЖШЪЧЗёДцдкзюДѓжЕЃПДцдкЕФЛАЃЌЧѓГіЦфзюДѓжЕКЭДЫЪБЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ3ЃЉШєвд![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЮЊЖЅЕуЕФЫФБпаЮЮЊЦНааЫФБпаЮЃЌЧѓЕу
ЮЊЖЅЕуЕФЫФБпаЮЮЊЦНааЫФБпаЮЃЌЧѓЕу![]() ЕФЫљгазјБъЃЎ
ЕФЫљгазјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПОнБЈЕРЃЌЁАЙњМЪМєЕЖЪЏЭЗВМаЛсЁБЬсвщНЋЁАМєЕЖЪЏЭЗВМЁБзїЮЊАТдЫЛсБШШќЯюФПЃЎФГаЃбЇЩњЛсЯыжЊЕРбЇЩњЖдетИіЬсвщЕФСЫНтГЬЖШЃЌЫцЛњГщШЁВПЗжбЇЩњНјааСЫвЛДЮЮЪОэЕїВщЃЌВЂИљОнЪеМЏЕНЕФаХЯЂНјааСЫЭГМЦЃЌЛцжЦСЫЯТУцСНЗљЩаВЛЭъећЕФЭГМЦЭМЃЎЧыФуИљОнЭГМЦЭМжаЫљЬсЙЉЕФаХЯЂНтД№ЯТСаЮЪЬтЃЎ
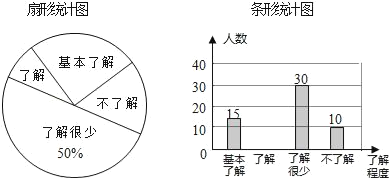
ЃЈ1ЃЉНгЪмЮЪОэЕїВщЕФбЇЩњЙВгаЁЁ ЁЁУћЃЌЩШаЮЭГМЦЭМжаЁАЛљБОСЫНтЁБВПЗжЫљЖдгІЩШаЮЕФдВаФНЧЮЊЁЁ ЁЁЃЛЧыВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ2ЃЉШєИУаЃЙВгабЇЩњ1200ШЫЃЌЧыИљОнЩЯЪіЕїВщНсЙћЃЌЙРМЦИУаЃбЇЩњжаЖдНЋЁАМєЕЖЪЏЭЗВМЁБзїЮЊАТдЫЛсБШШќЯюФПЕФЬсвщДяЕНЁАСЫНтЁБЁБКЭЁАЛљБОСЫНтЁБГЬЖШЕФзмШЫЪ§ЃЛ
ЃЈ3ЃЉЁАМєЕЖЪЏЭЗВМЁББШШќЪБЫЋЗНУПДЮШЮвтГіЁАМєЕЖЁБЁЂЁАЪЏЭЗЁБЁЂЁАВМЁБетШ§жжЪжЪЦжаЕФвЛжжЃЌЙцдђЮЊЃКМєЕЖЪЄВМЃЌВМЪЄЪЏЭЗЃЌЪЏЭЗЪЄМєЕЖЃЌШєЫЋЗНГіЯжЯрЭЌЪжЪЦЃЌдђЫуДђЦНЃЎШєаЁИеКЭаЁУїСНШЫжЛБШШќвЛОжЃЌЧыгУЪїзДЭМЛђСаБэЗЈЧѓСНШЫДђЦНЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com