
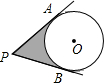
 如图,从P点引⊙O的两切线PA、PA、PB,A、B为切点,已知⊙O的半径为3,∠P=60°,则图中阴影部分的面积为( )
如图,从P点引⊙O的两切线PA、PA、PB,A、B为切点,已知⊙O的半径为3,∠P=60°,则图中阴影部分的面积为( )| A. | 9$\sqrt{3}$-3π | B. | 9$\sqrt{3}$-2π | C. | $\frac{9}{2}\sqrt{3}-3π$ | D. | $\frac{9}{2}\sqrt{3}-2π$ |
分析 如果连接OA、OB、OP,那么阴影部分的面积可以用两个直角三角形的面积和圆心角为120°的扇形的面积差来求得.
解答 解:连接OA,OB,OP,则∠OAP=∠OBP=90°,
∴∠AOB=180°-60°=120°,∠AOP=∠BOP=60°;
由切线长定理知,AP=PB=AOtan60°=3$\sqrt{3}$,
∴S阴影=S△APO+S△OPB-S扇形OAB;
即:S阴影=2×$\frac{1}{2}$×OA•AP-$\frac{120π×{3}^{2}}{360}$=9$\sqrt{3}$-3π.
故选A.
点评 本题考查了切线长定理以及直角三角形、扇形的面积的求法,关键是根据阴影部分的面积可以用两个直角三角形的面积和圆心角为120°的扇形的面积差解答.


科目:初中数学 来源: 题型:选择题
| A. | 在公园调查了1000名老年人的健康状况 | |
| B. | 调查了10名老年人的健康状况 | |
| C. | 在医院调查了1000名老年人的健康状况 | |
| D. | 利用派出所的户籍网随机调查了该地区10%的老年人健康状况 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
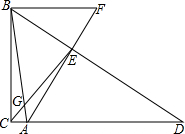 如图,在Rt△ABC中,∠ACB=90°,AC=1,BC=7,点D是边CA延长线的一点,AE⊥BD,垂足为点E,AE的延长线交CA的平行线BF于点F,连结CE交AB于点G.
如图,在Rt△ABC中,∠ACB=90°,AC=1,BC=7,点D是边CA延长线的一点,AE⊥BD,垂足为点E,AE的延长线交CA的平行线BF于点F,连结CE交AB于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9.05×106 | B. | 0.905×106 | C. | 0.905×107 | D. | 9.05×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
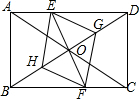 已知:如图,在矩形ABCD中,点E在边AD上,点F在边BC上,且AE=CF,作EG∥FH,分别与对角线BD交于点G、H,连接EH,FG.
已知:如图,在矩形ABCD中,点E在边AD上,点F在边BC上,且AE=CF,作EG∥FH,分别与对角线BD交于点G、H,连接EH,FG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com