
【题目】如图,以已知线段![]() 为弦作⊙
为弦作⊙![]() ,使其经过已知点
,使其经过已知点![]() .
.
(![]() )利用直尺和圆规作圆(保留作图痕迹,不必写出作法).
)利用直尺和圆规作圆(保留作图痕迹,不必写出作法).
(![]() )若
)若![]() ,
, ![]() ,求过
,求过![]() 、
、![]() 、
、![]() 三点的圆的半径.
三点的圆的半径.
![]()
【答案】(1)见解析;(2)16.9
【解析】试题分析:
(1)连接AC、BC,分别作AC、BC的垂直平分线,两条垂直平分线的交点为所求圆的圆心O,再连接OA,最后以点O为圆心,OA为半径作圆,所得的圆即所求的⊙O;
(2)如图,作OD⊥AB于点D,连接CD,由AC=BC可得![]() ,由此可得点C是
,由此可得点C是![]() 的中点,结合“垂径定理”可得点O、D、C在同一直线上,AD=
的中点,结合“垂径定理”可得点O、D、C在同一直线上,AD=![]() AB=12,在Rt△ADC中由勾股定理可求得CD的长为5;设半径OA=
AB=12,在Rt△ADC中由勾股定理可求得CD的长为5;设半径OA= ![]() ,则可得OD=
,则可得OD= ![]() ,在Rt△ADO中,由勾股定理建立方程,解方程可求得
,在Rt△ADO中,由勾股定理建立方程,解方程可求得![]() 的值即可.
的值即可.
试题解析:
(![]() )如下图中,⊙O即为所求圆;
)如下图中,⊙O即为所求圆;

(![]() )如图,作
)如图,作![]() 于点
于点![]() ,连接
,连接![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 为
为![]() 的中点,连接
的中点,连接![]() ,则
,则 ![]() 、
、![]() 、
、![]() 共线,
共线, ![]() ,
, ![]() ,
,
∴![]() ,
,
设半径![]() ,则在Rt△ADO中,由勾股定理可得:
,则在Rt△ADO中,由勾股定理可得: ![]() ,
,
解得![]() .
.
即过A、B、C三点的圆的半径为16.9.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知:△ABC中,CA=CB, ∠ACB=90,D为△ABC外一点,且满足∠ADB=90
(1)如图所示,求证:DA+DB=![]() DC
DC

(2)如图所示,猜想DA.DB.DC之间有何数量关系?并证明你的结论.

(3)如图所示,过C作CH⊥BD于H,BD=6,AD=3,则CH= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湘潭市继2017年成功创建全国文明城市之后,又准备争创全国卫生城市.某小区积极响应,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买2个温馨提示牌和3个垃圾箱共需550元,且垃圾箱的单价是温馨提示牌单价的3倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放48个垃圾箱,如果购买温馨提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中:A(1,1),B(-1,1),C(-1,-2),D(1,-2),现把一条长为2 018个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A→B→C→D→A→…的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)画出△A1B1C1沿x轴向右平移4个单位长度后得到的△A2B2C2;
(3)如果AC上有一点M(a,b)经过上述两次变换,那么对应A2C2上的点M2的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1+∠2=180°,∠B=∠3.

(1)判断DE与BC的位置关系,并说明理由:
解:结论:______________.
理由:∵∠1+∠2=180°,
∴_________________
∴∠ADE=∠3,
∵∠B=∠3
∴______________
∴DE∥BC;
(2)若∠C=65°,求∠DEC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,已知A(2,2)、B(4,0),若在x轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是( )
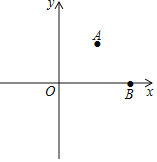
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依此为2,4,6,8,...,顶点依此用A1,A2,A3,A4......表示,则顶点A55的坐标是___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)自主阅读:在三角形的学习过程,我们知道三角形一边上的中线将三角形分成了两个面积相等三角形,原因是两个三角形的底边和底边上的高都相等,在此基础上我们可以继续研究:如图1,AD∥BC,连接AB,AC,BD,CD,则S△ABC=S△BCD.
证明:分别过点A和D,作AF⊥BC于F.DE⊥BC于E,由AD∥BC,可得AF=DE,又因为S△ABC=![]() ×BC×AF,S△BCD=
×BC×AF,S△BCD=![]() ×BC×DE .
×BC×DE .
所以S△ABC=S△BCD
由此我们可以得到以下的结论:像图1这样.
(2)问题解决:如图2,四边形ABCD中,AB∥DC,连接AC,过点B作BE∥AC,交DC延长线于点E,连接点A和DE的中点P,请你运用上面的结论证明:SABCD=S△APD
(3)应用拓展:
如图3,按此方式将大小不同的两个正方形放在一起,连接AF,CF,若大正方形的面积是80cm2,则图中阴影三角形的面积是 cm2.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com