
【题目】将下列推证过程补充完整. 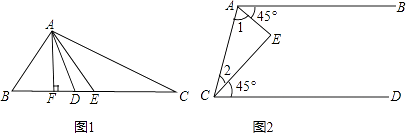
(1)如图1,在△ABC中,AE是中线,AD是角平分线,AF是高.
①BE== ![]() ;
;
②∠BAD== ![]() ;
;
③∠AFB==90°;
④S△ABC= .
(2)如图2,AB∥CD,∠BAE=∠DCE=45°,
∵AB∥CD
∴∠1+45°+∠2+45°= .
∴∠1+∠2= .
∴∠E= .
【答案】
(1)CE;BC;∠CAD;∠BAC;∠AFC;![]() BC?AF
BC?AF
(2)180°;90°;90°
【解析】解:(1)①BE=CE= ![]() BC;
BC;
②∠BAD=∠CAD= ![]() ∠BAC;
∠BAC;
③∠AFB=∠AFC=90°;
④S△ABC= ![]() BCAF;(2)∵AB∥CD,
BCAF;(2)∵AB∥CD,
∴∠1+45°+∠2+45°=180°,
∴∠1+∠2=90°,
∴∠E=90°.
所以答案是:(1)CE,BC;∠CAD,∠BAC;∠AFC; ![]() BCAF;(2)180°,90°,90°.
BCAF;(2)180°,90°,90°.
【考点精析】关于本题考查的平行线的性质和三角形的“三线”,需要了解两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;1、三角形角平分线的三条角平分线交于一点(交点在三角形内部,是三角形内切圆的圆心,称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部,是三角形的几何中心,称为中心);3、三角形的高线是顶点到对边的距离;注意:三角形的中线和角平分线都在三角形内才能得出正确答案.


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
【题目】景区售出的门票分为成人票和儿童票,购买3张成人票和1张儿童票共需350元,购买1张成人票和2张儿童票共需200元.
(1)求成人票和儿童票的单价;
(2)若干家庭结伴到该景区旅游,成人和儿童共30人.售票处规定:一次性购票数量达到30张,可购买团体票,每张票均按成人票价的八折出售,请你帮助他们选择花费最少的购票方式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖在二次函数y=2x2+4x+5的图象上,依横坐标找到三点(﹣1,y1),(2,y2),(﹣3,y3),则你认为y1 , y2 , y3的大小关系应为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为
的边长为![]() ,
, ![]() 、
、![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 、
、![]() 边上的动点(不含端点),且
边上的动点(不含端点),且![]() 、
、![]() 均过正方形的中心
均过正方形的中心![]() .
.
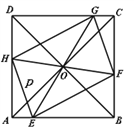
(1)填空: ![]()
![]() (“>”、“<”、“=”);
(“>”、“<”、“=”);
(2)当四边形![]() 为矩形时,请问线段
为矩形时,请问线段![]() 与
与![]() 应满足什么数量关系;
应满足什么数量关系;
(3)当四边形![]() 为正方形时,
为正方形时, ![]() 与
与![]() 交于点
交于点![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a>0)图象的对称轴为直线x=1,且经过点(﹣1,y1),(2,y2),则y1_____y2.(填“>”“<”或“=”)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com