
【题目】如图,在![]() 中,对角线
中,对角线![]() ,
,![]() 交于点
交于点![]() ,
,![]() 为
为![]() 的中点,点
的中点,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() .
.
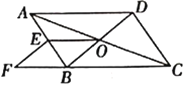
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)当线段![]() 和
和![]() 之间满足什么条件时,四边形
之间满足什么条件时,四边形![]() 是矩形?并说明理由;
是矩形?并说明理由;
(3)当线段![]() 和
和![]() 之间满足什么条件时,四边形
之间满足什么条件时,四边形![]() 是正方形?并说明理由.
是正方形?并说明理由.
【答案】(1)详见解析;(2)详见解析;(3)详见解析
【解析】
(1)首先证明OE是△ABC的中位线,推出OE∥BC,由EF∥OB,推荐可提出四边形OBFE是平行四边形.
(2)当AD⊥BD时,四边形OBFE是矩形.只要证明∠EOB=90°即可解决问题;
(3)当AD⊥BD,AD=BD时,四边形OBFE是正方形.根据中位线性质再证OB=OE即可.
(1)证明:∵四边形ABCD是平行四边形,
∴点O是AC的中点.
又∵点E是边AB的中点,
∴OE是△ABC的中位线,
∴OE∥BC,
又∵点F在CB的延长线上,
∴OE∥BF.
∵EF∥BD,即EF∥OB,
∴四边形OBFE是平行四边形.

(2)当AD⊥BD时,四边形OBFE是矩形.
理由:由(1)可知四边形OBFE是平行四边形,
又∵AD⊥BD,AD∥BC,且点F在BC的延长线上,
∴FC⊥BD,
∴∠OBF=90°,
∴四边形OBFE是矩形.
(3)结论:当AD⊥BD,AD=BD时,四边形OBFE是正方形.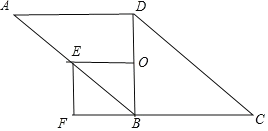
理由:∵OE为△ABD的中位线,
∴OE=![]() AD
AD
∵O为BD中点,
∴OB=![]() BD,
BD,
∵AD=BD,
∴OB=OE,
∵当AD⊥BD时,四边形OBFE是矩形,
∴当AD⊥BD,AD=BD时,四边形OBFE是正方形.


科目:初中数学 来源: 题型:
【题目】某地区果农收获草莓30吨,枇杷13吨,现计划租用甲、乙两种货车共10辆将这批水果全部运往省城,已知甲种货车可装草莓4吨和枇杷1吨,乙种货车可装草莓、枇杷各2吨.
(1)该果农安排甲、乙两种货车时有几种方案请您帮助设计出来;
(2)若甲种货车每辆要付运输费2 000元,乙种货车每辆要付运输费1 300元,则该果农应选择哪种运输方案才能使运费最少,最少运费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,把矩形![]() 放在平面直角坐标系中,边
放在平面直角坐标系中,边![]() 在
在![]() 轴上,边
轴上,边![]() 在
在![]() 轴上,连接
轴上,连接![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() 平分
平分![]() 交
交![]() 于点
于点![]() .动点
.动点![]() 在线段
在线段![]() 上运动,过
上运动,过![]() 作
作![]() 交
交![]() 于
于![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() .
.
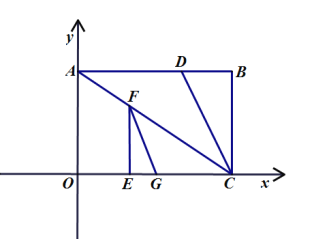
(1)当![]() 时,在线段
时,在线段![]() 上有一动点
上有一动点![]() ,
,![]() 轴上有一动点
轴上有一动点![]() ,连接
,连接![]() 当
当![]() 周长最小时,求
周长最小时,求![]() 周长的最小值及此时点
周长的最小值及此时点![]() 的坐标;
的坐标;
(2)如图2,在(1)问的条件下,点![]() 是直线
是直线![]() 上的一个动点,问:在
上的一个动点,问:在![]() 轴上是否存在
轴上是否存在![]() 点,使得
点,使得![]() 是以
是以![]() 为腰的等腰直角三角形?若存在,请直接写出
为腰的等腰直角三角形?若存在,请直接写出![]() 点及对应的
点及对应的![]() 点的坐标,若没有,请说明理由.
点的坐标,若没有,请说明理由.
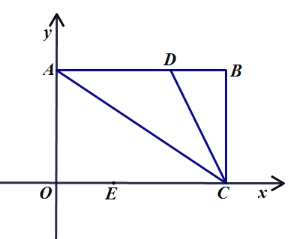
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校“阳光体育”活动的开展情况,从该校1000名学生中随机抽取部分学生进行问卷调查(每名学生只能填写一项自己最喜欢的体育项目),并将调查结果绘制成如图所示的两幅不完整的统计图,根据图中信息,解答下列问题:
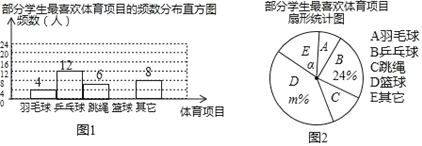
(1)被调查的学生共有多少人?
(2)扇形统计图中m的值和a的度数分别是多少?
(3)根据部分学生最喜欢体育项目的调查情况,请估计全校学生中最喜欢篮球的人数大约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC= ![]() ,反比例函数y=
,反比例函数y= ![]() 的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于 .
的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每一个小正方形边长都是1,每个小格的顶点叫作格点,以格点为顶点分别按下列要求画图.
(1)画出一个周长为24,面积为24的直角三角形;
(2)画出一个周长为20,面积为24的菱形;


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k<0)的图象经过点C(3,0),且与两坐标轴围成的三角形的面积为3.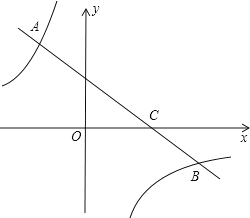
(1)求该一次函数的解析式;
(2)若反比例函数y=![]() 的图象与该一次函数的图象交于二、四象限内的A、B两点,且AC=2BC,求m的值.
的图象与该一次函数的图象交于二、四象限内的A、B两点,且AC=2BC,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com