
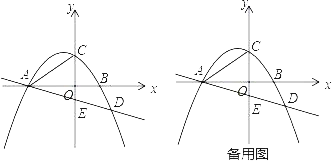
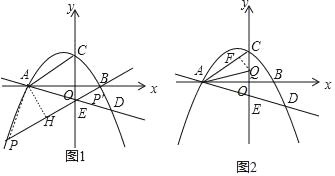
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2﹣![]() x+c与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,直线y=﹣
x+c与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,直线y=﹣![]() x+b与抛物线相交于点A,D,与y轴交于点E,已知OB=
x+b与抛物线相交于点A,D,与y轴交于点E,已知OB=![]() ,OC=2.
,OC=2.
(1)求a,b,c的值;
(2)点P是抛物线上的一个动点,若直线PE∥AC,连接PA、PE,求tan∠APE的值;
(3)动点Q从点C出发,沿着y轴的负方向运动,是否存在某一位置,使得∠OAQ+∠OAD=30°?若存在,请求出点Q的坐标;若不存在,请说明理由.
【答案】(1)![]() ,b=-1,c=2;(2)
,b=-1,c=2;(2)![]() ;(3)点Q的坐标为(0,
;(3)点Q的坐标为(0,![]() )或(0,﹣
)或(0,﹣![]() ).
).
【解析】
(1)先确定B、C点坐标,再利用待定系数法求抛物线解析式得到a、c的值,然后解方程
﹣![]() x2﹣
x2﹣![]() x+2=0得A(﹣2
x+2=0得A(﹣2![]() ,0),然后把A点坐标代入y=﹣
,0),然后把A点坐标代入y=﹣![]() x+b得b的值;
x+b得b的值;
(2)易得直线AC的解析式为y=![]() x+2,E(0,1),利用直线平移得到直线PE的解析式为y=
x+2,E(0,1),利用直线平移得到直线PE的解析式为y=![]() x﹣1,则解方程组
x﹣1,则解方程组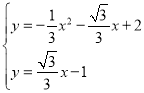 得P点坐标为(3
得P点坐标为(3![]() ,4)或
,4)或
(![]() ,0);当P点坐标为(
,0);当P点坐标为(![]() ,0),即P点与B点重合,易得tan∠APE=
,0),即P点与B点重合,易得tan∠APE=![]() ,此时∠ABH=30°;当P点坐标为(3
,此时∠ABH=30°;当P点坐标为(3![]() ,4)时,作AH⊥PE于H,根据面积法求出PH,然后根据正切定义计算tan∠APH的值;
,4)时,作AH⊥PE于H,根据面积法求出PH,然后根据正切定义计算tan∠APH的值;
(3)先计算出∠CAO=30°,∠ACO=60°,AC=2OC=4,则可判断∠CAQ=∠OAD,作QF⊥AC于F,如图,设Q(0,t),利用三角函数的定义得到CQ=2t,CF=![]() CF=
CF=![]() , FQ=
, FQ=![]() ,则AF=3+
,则AF=3+![]() t,通过Rt△AQF∽Rt△AEO得
t,通过Rt△AQF∽Rt△AEO得![]() (2﹣t):1=(3+
(2﹣t):1=(3+![]() t):
t):![]() ,解方程求出t得到此时Q点的坐标,易得Q(0,
,解方程求出t得到此时Q点的坐标,易得Q(0,![]() )关于x轴的对称点(0,
)关于x轴的对称点(0,![]() )也满足条件.
)也满足条件.
解:(1)∵OB=![]() ,OC=2,
,OC=2,
∴B(![]() ,0),C(0,2),
,0),C(0,2),
把B(![]() ,0),C(0,2)代入y=ax2﹣
,0),C(0,2)代入y=ax2﹣![]() x+c得
x+c得![]() ,解得
,解得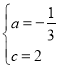 ,
,
∴抛物线解析式为y=﹣![]() x2﹣
x2﹣![]() x+2,
x+2,
当y=0时,﹣![]() x2﹣
x2﹣![]() x+2=0,解得x1=﹣2
x+2=0,解得x1=﹣2![]() ,x2=
,x2=![]() ,则A(﹣2
,则A(﹣2![]() ,0),
,0),
把A(﹣2![]() ,0)代入y=﹣
,0)代入y=﹣![]() x+b得﹣1+b=0,解得b=﹣1;
x+b得﹣1+b=0,解得b=﹣1;
(2)易得直线AC的解析式为y=![]() x+2,E(0,﹣1),
x+2,E(0,﹣1),
∵直线PE∥AC,
∴直线PE的解析式为y=![]() x﹣1,
x﹣1,
解方程组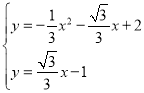 得
得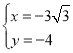 或
或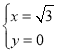 ,则P点坐标为(﹣3
,则P点坐标为(﹣3![]() ,﹣4)或(
,﹣4)或(![]() ,0);
,0);
当P点坐标为(![]() ,0),即P点与B点重合,tan∠APE=
,0),即P点与B点重合,tan∠APE=![]() =
=![]() ,此时∠ABH=30°,
,此时∠ABH=30°,
当P点坐标为(﹣3![]() ,﹣4)时,作AH⊥PE于H,如图2,
,﹣4)时,作AH⊥PE于H,如图2,
PB=![]() =8,
=8,
∵S△APB=![]() ,
,
∴AH=![]() ,
,
∴BH=![]() ,
,
∴PH=8﹣![]() ,
,
在Rt△APH中,tan∠APH=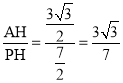 ,
,
综上所述,tan∠APE的值为![]() 或
或![]() ;
;
(3)存在.
如图2,在Rt△OAC中,tan∠OAC=![]() ,
,
∴∠CAO=30°,∠ACO=60°,
∴AC=2OC=4,
∵∠OAQ+∠OAD=30°,
∴∠CAQ=∠OAD,
作QF⊥AC于F,如图,设Q(0,t),
在Rt△CQF中,CQ=2﹣t,CF=![]() CF=
CF=![]() ,FQ=
,FQ=![]() ,
,
∴AF=AC﹣CF=4﹣![]() =3+
=3+![]() t,
t,
∵∠QAF=∠OAE,
∴Rt△AQF∽Rt△AEO,
∴FQ:OE=AF:AO,即![]() (2﹣t):1=(3+
(2﹣t):1=(3+![]() t):
t):![]() ,解得t=
,解得t=![]() ,此时Q(0,
,此时Q(0,![]() ),
),
易得Q(0,![]() )关于x轴的对称点(0,﹣
)关于x轴的对称点(0,﹣![]() )也满足条件,
)也满足条件,
综上所述,点Q的坐标为(0,![]() )或(0,﹣
)或(0,﹣![]() ).
).


科目:初中数学 来源: 题型:
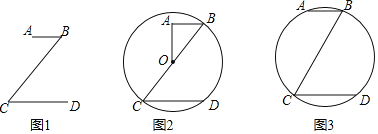
【题目】如图1,有一个“z”字图形,其中AB∥CD,AB:CD:BC=1:2:3.
(1)如图2,若以BC为直径的⊙O恰好经过点D,连结AO.
①求cosC.
②当AB=2时,求AO的长.
(2)如图3,当A,B,C,D四点恰好在同一个圆上时.求∠C的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在三角形ABC中,∠ACB=90°,AC=6,BC=8,点D为边BC的中点,射线DE⊥BC交AB于点E.点P从点D出发,沿射线DE以每秒1个单位长度的速度运动.以PD为斜边,在射线DE的右侧作等腰直角△DPQ.设点P的运动时间为t(秒).
(1)用含t的代数式表示线段EP的长.
(2)求点Q落在边AC上时t的值.
(3)当点Q在△ABC内部时,设△PDQ和△ABC重叠部分图形的面积为S(平方单位),求S与t之间的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《如果想毁掉一个孩子,就给他一部手机!》这是2017年微信圈一篇热传的文章.国际上,法国教育部宣布从 2018 年9月新学期起小学和初中禁止学生使用手机.为了解学生手机使用情况,某学校开展了“手机伴我健康行”主题活动,他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查,并绘制成如图①,②的 统计图,已知“查资料”的人数是 40人.请你根据以上信息解答下列问题:
(1)在扇形统计图中,“玩游戏”对应的百分比为______,圆心角度数是______度;
(2)补全条形统计图;
(3)该校共有学生2100人,估计每周使用手机时间在2 小时以上(不含2小时)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)在Rt△ABC中,∠BAC=![]() ,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.

(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元旦节前夕,某花店购进康乃馨和玫瑰两种鲜花,销售过程中发现康乃馨比玫瑰销量大,店主决定将玫瑰每枝降价2元促销,降价后80元可购买玫瑰的数量是原来可购买玫瑰数量的1.25倍.
(1)试问:降价后每枝玫瑰的售价是多少元?
(2)根据销售情况,店主用不多于1000元的资金再次购进两种鲜花共180枝,康乃馨进价为6元/枝,玫瑰的进价是5元/枝。试问;至少需要购进多少枝玫瑰?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,分析下列四个结论:①abc<0;②b2-4ac>0;③a+b+c>0;④a-b+c>0.其中正确的结论有( )
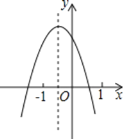
A. 1个
B. 2个
C. 3个
D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
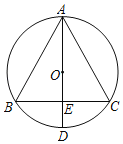
【题目】如图,△ABC内接于⊙O,AD为⊙O的直径,AD与BC相交于点E,且BE=CE.
(1)请判断AD与BC的位置关系,并说明理由;
(2)若BC=6,ED=2,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
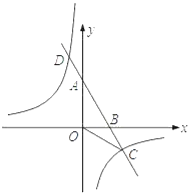
【题目】如图,已知A、B两点的坐标分别为A(0,2![]() ),B(2,0),直线AB与反比例函数y=
),B(2,0),直线AB与反比例函数y=![]() 的图象交于点C和点D(﹣1,a).
的图象交于点C和点D(﹣1,a).
(1)求直线AB和反比例函数的解析式;
(2)求∠ACO的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com