
����Ŀ����ͼ�٣���������ABC�У���ACB=90����AC=6��BC=8����DΪ��BC���е㣬����DE��BC��AB�ڵ�E����P�ӵ�D������������DE��ÿ��1����λ���ȵ��ٶ��˶�����PDΪб�ߣ�������DE���Ҳ�������ֱ����DPQ�����P���˶�ʱ��Ϊt���룩��
��1���ú�t�Ĵ���ʽ��ʾ�߶�EP�ij���
��2�����Q���ڱ�AC��ʱt��ֵ��
��3������Q����ABC�ڲ�ʱ������PDQ����ABC�ص�����ͼ�ε����ΪS��ƽ����λ������S��t֮��ĺ�����ϵʽ��

���𰸡���1������P���߶�DE��ʱ��EP =3-t������P��DE���ӳ�����ʱ��EP= t-3����2��t=8s����3��S=
��������
��1������������������ۣ���P���߶�DE�ϣ���P��DE���ӳ����ϣ������߶εĺͲ��ϵ���м��㣻
��2������Q���ڱ�AC��ʱ������Q��QF��DP��F�������ı���CDFQ�Ǿ��Σ���DPQ�ǵ���ֱ�������Σ����DP��2FQ��8�����ɵõ�t��ֵ��
��3������������������ۣ��ٵ���P���߶�DE��ʱ����PDQ����ABC�ص�����Ϊ��DPQ���ڵ���P���߶�DE���ӳ�����ʱ����PDQ����ABC�ص�����Ϊ�ı���EDQG���ֱ����S��t֮��ĺ�����ϵʽ��
�⣺��1������ɵã�DP=t��DE=![]() AC=3��
AC=3��
����P���߶�DE��ʱ��EP=DE-DP=3-t��
����P��DE���ӳ�����ʱ��EP=DP-DE=t-3��
��2����ͼ��ʾ������Q���ڱ�AC��ʱ������Q��QF��DP��F��

�ߡ�C=��CDF=��DFQ=90����
���ı���CDFQ�Ǿ��Σ�
��FQ=CD=![]() BC=4��
BC=4��
�ߡ�DPQ�ǵ���ֱ�������Σ�
��DP=2FQ=8��
��t=![]() =8��s����
=8��s����
��3���ٵ���P���߶�DE��ʱ����PDQ����ABC�ص�����Ϊ��DPQ����DP=t��DP���ϵĸ�Ϊ![]() t��
t��

�ߵ�P�ӵ�D�˶�����E��ʱ��ʱ��Ϊ3s��
�൱0��t��3ʱ��S=![]() ��t��
��t��![]() t=
t=![]() ��
��
�ڵ���P���߶�DE���ӳ�����ʱ����PDQ����ABC�ص�����Ϊ�ı���EDQG��
��ͼ��ʾ����G��GF��PE��F������GFE�ס�BCA����PF=GF��

��AC=6��BC=8��
��EF��FG=3��4��EF��FP=3��4��
��PE=t-3��
��FG=![]() ��t-3����
��t-3����
���PEG�����=![]() ��PE��FG=
��PE��FG=![]() ��
��![]() ��t-3��2��
��t-3��2��
�ɣ�2����֪����Q���ڱ�AC��ʱ��t��ֵΪ8s��
�൱3��t��8ʱ��S=![]() t2-
t2-![]() ��
��![]() ��t-3��2=
��t-3��2=![]() ��
��
����������S��t֮��ĺ�����ϵʽΪ��S= ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��P��m��n����������y=ax2-4ax��a��0���ϣ�EΪ�����ߵĶ��㣮
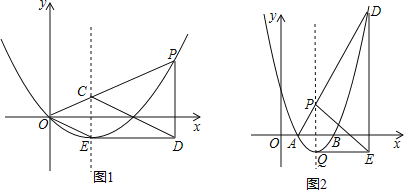
��1�����E�����꣨�ú�a��ʽ�ӱ�ʾ����
��2������P�ڵ�һ���ޣ��߶�OP�������ߵĶԳ����ڵ�C���������ߵĶ���E��x���ƽ����DE������P��x��Ĵ��߽�DE�ڵ�D������CD����֤��CD��OE��
��3����ͼ2����a=1���ҽ�ͼ1�е�����������ƽ��3����λ����x�ύ��A��B���㣬ƽ�ƺ�������ߵĶ���ΪQ��P����x���Ϸ��ĶԳ����ϵĶ��㣬ֱ��AP������������һ��D���ֱ��Q��D��x�ᡢy���ƽ���߽��ڵ�E���ҡ�EPQ=2��APQ�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
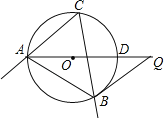
����Ŀ����ͼ����O�ǡ�ABC�����Բ����C��60�㣬AD����O��ֱ����Q��AD�ӳ����ϵ�һ�㣬��BQ��AB��
��1����֤��BQ����O�����ߣ�
��2����AQ��6��
������O�İ뾶��
��P���ӻ�AB�ϵ�һ�����㣬����P��EF��AB��EF�ֱ�CA��CB���ӳ�����E��F���㣬����OP����OP��AB֮����ʲôλ�ù�ϵʱ���߶�EFȡ�����ֵ���жϲ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() ABC�����Բ��ABΪֱ������BAC��ƽ���߽�
ABC�����Բ��ABΪֱ������BAC��ƽ���߽�![]() �ڵ�D������D��DE
�ڵ�D������D��DE![]() AC�ֱ�AC��AB���ӳ����ڵ�E��F��
AC�ֱ�AC��AB���ӳ����ڵ�E��F��
��1����֤��EF��![]() �����ߣ�
�����ߣ�
��2����AC=4��CE=2����![]() �ij��ȣ����������
�ij��ȣ����������![]() ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
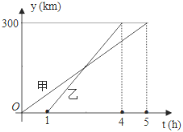
����Ŀ���ס���������A�dz���������ʻ��B�ǣ���������ʻ�����У��ס��������뿪A�ǵľ���y��ǧ�ף���׳���ʻʱ��x��Сʱ��֮��ĺ�����ϵ��ͼ��ʾ������ͼ���ṩ����Ϣ������������⣺
��1��A��B������� ǧ�ף�
��2���ֱ���ס��������뿪A�ǵľ���y��x�Ĺ�ϵʽ��
��3�����ҳ�������Сʱ�ϼ׳���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
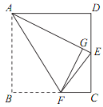
����Ŀ����ͼ����������ֽƬ ABCD �У� E �� CD ���е㣬��������ֽƬ�۵����� B �����߶�AE �ϵĵ� G �����ۺ�Ϊ AF ���� AD��4 cm���� CF �ij�Ϊ___________cm ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������
��ͼ��ͼ����һ���������߳�Ϊ 1 ��С��������ɵġ�L����ֽƬ��ͼ����һ�� a�� b �ķ���ֽ��a�� b�ķ���ָֽ�߳��ֱ�Ϊ a��b �ľ��Σ����ֳ� a�� b���߳�Ϊ 1 ��С�����Σ����� a��2 �� b��2���� a��b Ϊ�������� ����ͼ�ٷ�����ͼ���У�ʹ��ǡ�ø�סͼ���е�����С�����Σ����ж����ֲ�ͬ�ķ��÷�����
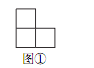
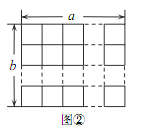
����̽����
Ϊ̽�����ɣ����Dz���һ���������⻯�IJ��ԣ��ȴ�����������֣�����εݽ������ó�һ���ԵĽ��ۣ�
̽��һ��
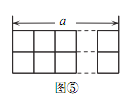
��ͼ�ٷ����� 2�� 2�ķ���ֽ�У�ʹ��ǡ�ø�ס���е�����С�����Σ����ж����ֲ�ͬ�ķ��÷�����
��ͼ�ۣ����� 2��2�ķ���ֽ��Ҫ��ͼ�ٸ�ס���е�����С�����Σ���Ȼ�� 4 �ֲ�ͬ�ķ��÷�����
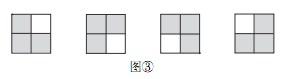
̽������
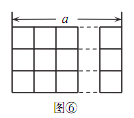
��ͼ�ٷ����� 3��2�ķ���ֽ�У�ʹ��ǡ�ø�ס���е�����С�����Σ����ж����ֲ�ͬ�ķ��÷�����
��ͼ�ܣ��� 3��2�ķ���ֽ�У��������ҵ� 2 ��λ�ò�ͬ�� 2 ��2��������̽��һ�Ľ��ۿ�֪����ͼ�ٷ����� 3��2 �ķ���ֽ�У�ʹ��ǡ�ø�ס���е�����С�����Σ����� 2 ��4��8��
��ͬ�ķ��÷�����
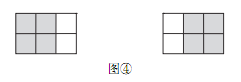
̽������
��ͼ�ٷ����� a ��2 �ķ���ֽ�У�ʹ��ǡ�ø�ס���е�����С�����Σ����ж����ֲ�ͬ�ķ��÷�����
��ͼ�ݣ� �� a ��2 �ķ���ֽ�У��������ҵ�______��λ�ò�ͬ�� 2��2��������̽��һ�Ľ��ۿ�֪����ͼ�ٷ����� a�� 2 �ķ���ֽ�У�ʹ��ǡ�ø�ס���е�����С�����Σ�����______�ֲ�ͬ�ķ��÷�����
̽���ģ�
��ͼ�ٷ����� a ��3 �ķ���ֽ�У�ʹ��ǡ�ø�ס���е�����С�����Σ����ж����ֲ�ͬ�ķ��÷�����
��ͼ�ޣ��� a ��3 �ķ���ֽ�У��������ҵ�______��λ�ò�ͬ�� 2��2��������̽��һ�Ľ��ۿ�֪����ͼ�ٷ����� a ��3 �ķ���ֽ�У�ʹ��ǡ�ø�ס���е�����С�����Σ�����_____�ֲ�ͬ�ķ��÷�����
����
��������
��ͼ�ٷ����� a ��b�ķ���ֽ�У�ʹ��ǡ�ø�ס���е�����С�����Σ����ж����ֲ�ͬ�ķ��÷�����������ǰ���̽��������д�������̣����軭ͼ����
������չ��
��ͼ��ͼ����һ���� 4 ���ⳤΪ 1 ��С�����幹�ɵļ����壬ͼ����һ�����������߷ֱ�Ϊ a��b ��c ��a��2 �� b��2 �� c��2 ���� a��b��c �����������ij����壬���ֳ���a��b��c���ⳤΪ 1 ��С�����壮��ͼ��IJ�ͬλ�ù������ҵ�______��ͼ�������ļ����壮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
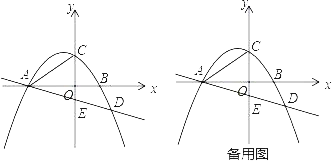
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�������y��ax2��![]() x+c��x���ཻ��A��B���㣨��A�ڵ�B����ࣩ����y���ཻ�ڵ�C��ֱ��y����
x+c��x���ཻ��A��B���㣨��A�ڵ�B����ࣩ����y���ཻ�ڵ�C��ֱ��y����![]() x+b���������ཻ�ڵ�A��D����y�ύ�ڵ�E����֪OB��
x+b���������ཻ�ڵ�A��D����y�ύ�ڵ�E����֪OB��![]() ��OC��2��
��OC��2��
��1����a��b��c��ֵ��
��2����P���������ϵ�һ�����㣬��ֱ��PE��AC������PA��PE����tan��APE��ֵ��
��3������Q�ӵ�C����������y��ĸ������˶����Ƿ����ijһλ�ã�ʹ�á�OAQ+��OAD��30�㣿�����ڣ��������Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
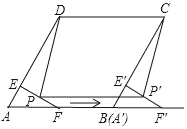
����Ŀ����ͼ��������ABCD�У���A��60����AD��4����F��AB���е㣬����F��FE��AD������ΪE������AEF�ص�A����B�ķ���ƽ�ƣ��õ���A'E'F'�����P��P'�ֱ���EF��E'F'���е㣬����A'���B�غ�ʱ���ı���PP'CD�����Ϊ��������
A. 7![]() B. 6
B. 6![]() C. 8
C. 8![]() D. 8
D. 8![]() ��4
��4
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com