
����Ŀ����ͼ1��P��m��n����������y=ax2-4ax��a��0���ϣ�EΪ�����ߵĶ��㣮
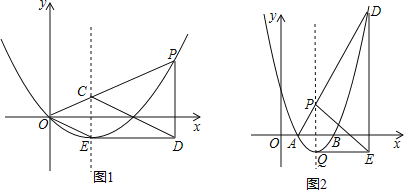
��1�����E�����꣨�ú�a��ʽ�ӱ�ʾ����
��2������P�ڵ�һ���ޣ��߶�OP�������ߵĶԳ����ڵ�C���������ߵĶ���E��x���ƽ����DE������P��x��Ĵ��߽�DE�ڵ�D������CD����֤��CD��OE��
��3����ͼ2����a=1���ҽ�ͼ1�е�����������ƽ��3����λ����x�ύ��A��B���㣬ƽ�ƺ�������ߵĶ���ΪQ��P����x���Ϸ��ĶԳ����ϵĶ��㣬ֱ��AP������������һ��D���ֱ��Q��D��x�ᡢy���ƽ���߽��ڵ�E���ҡ�EPQ=2��APQ�����P�����꣮
���𰸡�(1) E��2����4a����(2)������;(3) P��2��![]() +1����
+1����
��������
��1����ԭʽ��ȡ����ʽȻ�ɽ��
��2����ֱ��OE�Ľ���ʽΪ��y��k x����E�����ɵ�ֱ��OE�Ľ���ʽΪ��y����2ax����P��m��n����ֱ��OP�Ľ���ʽΪ��y��![]() ���õ�C��2��
���õ�C��2��![]() ����Ȼ����ֱ��CD�Ľ���ʽΪ��y��kx+b���õ���k����2a�����ɽ��
����Ȼ����ֱ��CD�Ľ���ʽΪ��y��kx+b���õ���k����2a�����ɽ��
��3����a��1ʱ�������߽���ʽΪ��y��x2��4x������ƽ��3����λ���µ������߽���ʽΪ��y��x2��4x+3����x��2��2��1��Ȼ����P��2��t�����ɵ�AP�Ľ���ʽΪ��y��tx��t��D��3+t��t2+2t����Q��2����1����E��3+t����1��������PE��x����F�����ɽ��
�⣺��1��y��ax2��4ax��a��x2��4x+4��4����a��x��2��2��4a��
��E��2����4a����
��2����ֱ��OE�Ľ���ʽΪ��y��kx��
��E��2����4a������ã�2k����4a��
k����2a��
��ֱ��OE�Ľ���ʽΪ��y����2ax��
��P��m��n����ֱ��OP�Ľ���ʽΪ��y��![]() ��
��
�൱x��2ʱ��y��![]() ����C��2��
����C��2��![]() ����
����
��D��m����4a����
��ֱ��CD�Ľ���ʽΪ��y��kx+b��
����D��C���������ã�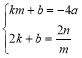 ��n��am2��4am����
��n��am2��4am����
��ã�k����2a��
������ֱ��ϵ����ȣ�
��OE��CD��
��3����ͼ2����a��1ʱ�������߽���ʽΪ��y��x2��4x��
����ƽ��3����λ���µ������߽���ʽΪ��y��x2��4x+3����x��2��2��1��
��Q��2����1����A��1��0����B��3��0����
��P��2��t����
�ɵ�AP�Ľ���ʽΪ��y��tx��t��
����������Ϊ��![]() ����ã�
����ã�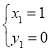 ��
��![]() ��
��
��D��3+t��t2+2t����
��Q��2����1����
��E��3+t����1����
��PQ��QE��t+1��
���EPQ��45�㣬
�ߡ�EPQ��2��APQ��
���APQ��22.5�㣬
��PE��x����F��
�ߡ�DEP��45�㣬
��ME��FM��1��
���FPA����PAF��67.5�㣬
��PF��AF��t+1��
��FP��![]() t��
t��
��![]() t��t+1��
t��t+1��
t��![]() ��
��![]() +1��
+1��
��P��2��![]() +1����
+1����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���������裬�û���ũ�ḻũ���ҵ����������Ͳʵ����磬���Ҿ����Թ���ʵ��ũ��ʵ�������������涨ÿ����һ̨�ʵ磬������������Ԫ��������ij�̳����۲ʵ�̨��y(̨)�벹�����![]() (Ԫ)֮�����������ͼ����ʾ��һ�κ�����ϵ�����Ų������
(Ԫ)֮�����������ͼ����ʾ��һ�κ�����ϵ�����Ų������![]() �IJ�������������Ҳ�������ӣ���ÿ̨�ʵ������
�IJ�������������Ҳ�������ӣ���ÿ̨�ʵ������![]() (Ԫ)����Ӧ������
(Ԫ)����Ӧ������![]() ��
��![]() ֮��Ҳ����������ͼ����ʾ��һ�κ�����ϵ��
֮��Ҳ����������ͼ����ʾ��һ�κ�����ϵ��
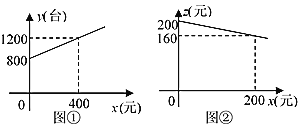
(1)������δ��̨������ʩǰ�����̳����۲ʵ���������Ϊ����Ԫ��
(2)��������������ʵʩ�ֱ�������̳����۲ʵ�̨��![]() ��ÿ̨�ҵ������
��ÿ̨�ҵ������![]() �������������
�������������![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
(3)Ҫʹ���̳����۲ʵ��������![]() (Ԫ)�������Ӧ��ÿ̨�������
(Ԫ)�������Ӧ��ÿ̨�������![]() ��Ϊ���٣������������
��Ϊ���٣������������![]() �����ֵ��
�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʵʩ�¿γ̸ĸ��ѧ��������ѧϰ���������������кܴ���ߣ�����ʦΪ���˽����̰༶ѧ������ѧϰ�����������ľ���������Ա��ಿ��ѧ��������Ϊ�ڰ���µĸ��ٵ��飬�����������ֳ����࣬A���ر�ã�B���ã�C��һ�㣻D���ϲ�������������Ƴ�����������������ͳ��ͼ���������ͳ��ͼ����������⣺
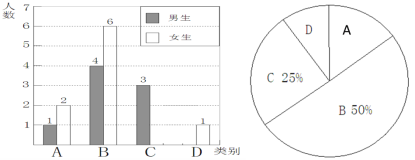
��1�����ε�����C��Ů���� ����D�������� ���������������ͳ��ͼ����������
��2����������ͳ��ͼ��D��ռ��Բ�Ľ��� ��
��3��Ϊ�˹�ͬ����������ʦ��ӱ������A���D��ѧ���зֱ�ѡȡһλͬѧ������һ��һ������ѧϰ�������б���������ͼ�ķ��������ѡ��λͬѧǡ����һλ��ͬѧ��һλŮͬѧ�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB=4cm��BC=8cm������M�ӵ�D������������D��C��B��A��D������2cm/s���ٶ��˶�������N�ӵ�D������������D��A��B��C��D������1cm/s���ٶ��˶���������M��Nͬʱ����������ʱֹͣ�˶�������E���߶�BC�ϣ���BE=3cm������_____���ӣ���A��E��M��N���ƽ���ı��Σ�
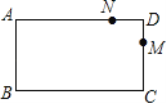
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֽ�ɻ������Ƕ�ʱ���ֵĻ��䣬����һ�ų�Ϊ290mm����Ϊ200mm�İ�ֽ����ͼ��ʾ�������漸�������۳�ֽ�ɻ�����˵������һ������ֽ����EF�۵���AB�ߵĶ�Ӧ��A��B�����CDƽ�У������ǵľ����Ϊx���ڶ�������EM��MF�ֱ�����MH��MG�۵���ʹEM��MF�غϣ��Ӷ���ñ�HG��A��B��ľ���ҲΪx������PD=______mm��
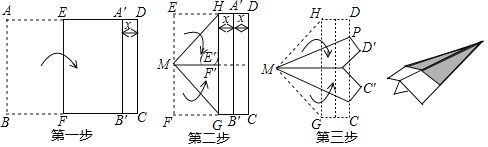
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ���ڼ䣬С�Ű��ݻ�Ϊ60��������������Լݳ��У���ʻһ��·�̺���������ͣ����Ϣ����Ϣ��С���뿪����������ǰ�У�Ϊ��˳������Ŀ�ĵأ�С���������Sǧ�ļ���վ����.��С�Ŵӳ����㵽��������Ϣ����ʻ��·��Ϊ200ǧ�ף������ڼ�ƽ���ͺ�Ϊÿǧ��0.12��.
(1)��С���뿪��������Ϣ��ʱ�������ڻ��ж���������?
(2)��С�Ŵ��뿪��������Ϣ�㵽�������վ�����ڼ��ƽ���ͺ�Ϊÿǧ��a������д��S��a�ĺ�����ϵʽ����0.08��a��0.1����S��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾����һ���������ͱ��±����ƻ���2000Ԫ������������2800Ԫ�����±�����֪һ�����±���һ����������10Ԫ���ù�˾����IJ������뱣�±�����������ͬ��
��1���������⣬������ͬѧ���ȼ���ù�˾����IJ������뱣�±�����������ͬ�����ֱ��г��ķ������£�![]() ��
��![]() ��
��![]() ��
��![]() ��10��������λͬѧ���еķ��̣�����ֱ�ָ��δ֪��x��y��ʾ�����壺x��ʾ ��y��ʾ ��
��10��������λͬѧ���еķ��̣�����ֱ�ָ��δ֪��x��y��ʾ�����壺x��ʾ ��y��ʾ ��
��2����ѡ����һ������˵���ù�˾����IJ������뱣�±��������ܷ���ͬ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
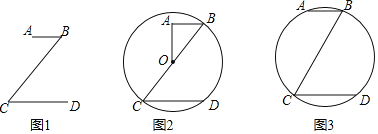
����Ŀ����ͼ1����һ����z����ͼ�Σ�����AB��CD��AB��CD��BC��1��2��3��
��1����ͼ2������BCΪֱ���ġ�Oǡ�þ�����D������AO��
����cosC��
�ڵ�AB��2ʱ����AO�ij���
��2����ͼ3����A��B��C��D�ĵ�ǡ����ͬһ��Բ��ʱ�����C�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣���������ABC�У���ACB=90����AC=6��BC=8����DΪ��BC���е㣬����DE��BC��AB�ڵ�E����P�ӵ�D������������DE��ÿ��1����λ���ȵ��ٶ��˶�����PDΪб�ߣ�������DE���Ҳ�������ֱ����DPQ�����P���˶�ʱ��Ϊt���룩��
��1���ú�t�Ĵ���ʽ��ʾ�߶�EP�ij���
��2�����Q���ڱ�AC��ʱt��ֵ��
��3������Q����ABC�ڲ�ʱ������PDQ����ABC�ص�����ͼ�ε����ΪS��ƽ����λ������S��t֮��ĺ�����ϵʽ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com