
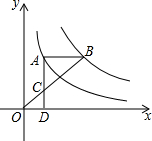
 如图,点A(m,3)在反比例函数y=$\frac{3}{x}$(x>0)的图象上,点B在反比例函数y=$\frac{k}{x}(x>0)$的图象上,AB∥x轴,过点A作AD⊥x轴于点D,连接OB与AD相交于点C,且AC=2CD.
如图,点A(m,3)在反比例函数y=$\frac{3}{x}$(x>0)的图象上,点B在反比例函数y=$\frac{k}{x}(x>0)$的图象上,AB∥x轴,过点A作AD⊥x轴于点D,连接OB与AD相交于点C,且AC=2CD.分析 (1)把A的坐标代入反比例函数的解析式即可求得.
(2)过点B作BE⊥x轴于E,延长线段BA,交y轴于F,得出四边形AFOD是矩形,四边形OEBF是矩形,得出S矩形AFOD=3,S矩形OEBF=k,根据平行线分线段成比例定理证得AB=2OD,即OE=3OD,即可求得矩形OEBF的面积,根据反比例函数系数k的几何意义即可求得k的值.
解答  解:(1)∵点A(m,3)在反比例函数y=$\frac{3}{x}$(x>0)的图象上,
解:(1)∵点A(m,3)在反比例函数y=$\frac{3}{x}$(x>0)的图象上,
∴3=$\frac{3}{m}$,解得m=1,
(2)过点B作BE⊥x轴于E,延长线段BA,交y轴于F,
∵AB∥x轴,
∴AF⊥y轴,
∴四边形AFOD是矩形,四边形OEBF是矩形,
∴AF=OD,BF=OE,
∴AB=DE,
∵点A在双曲线y=y=$\frac{3}{x}$(x>0)上,
∴S矩形AFOD=3,
同理S矩形OEBF=k,
∵AB∥OD,
∴$\frac{OD}{AB}$=$\frac{CD}{AC}$=$\frac{1}{2}$,
∴AB=2OD,
∴DE=2OD,
∴S矩形OEBF=3S矩形AFOD=9,
∴k=9,
∴反比例函数y=$\frac{k}{x}$的表达式为y=$\frac{9}{x}$.
点评 本题考查了反比例函数图象上点的坐标特征,反比例函数系数k的几何意义,矩形的判定和性质,平行线分线段成比例定理,作出辅助线,构建矩形是解题的关键.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:解答题
 某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:| 运动项目 | 频数(人数) | 频率 |
| 篮球 | 60 | 0.25 |
| 羽毛球 | m | 0.20 |
| 乒乓球 | 72 | n |
| 跳绳 | 36 | 0.15 |
| 其它 | 24 | 0.10 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3a3+4a3=7a6 | B. | 3a2•4a2=12a2 | C. | (a+2)2=a2+4 | D. | (a+b)(a-b)=a2-b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4.44×108 | B. | 4.44×1010 | C. | 4.44×1011 | D. | 4.44×1012 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2元 | B. | 2.5元 | C. | 3元 | D. | 5元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com