
����Ŀ����ͼ��������L��![]() ��x�ύ��A��B��3��0�����㣨A��B����ࣩ����y�ύ�ڵ�C��0��3������֪�Գ���x=1��
��x�ύ��A��B��3��0�����㣨A��B����ࣩ����y�ύ�ڵ�C��0��3������֪�Գ���x=1��
��1����������L�Ľ���ʽ��
��2����������L����ƽ��h����λ���ȣ�ʹƽ�ƺ����������ߵĶ���������OBC�ڣ�������OBC�ı߽磩����h��ȡֵ��Χ��
��3�����P��������L����һ�㣬��Q��ֱ��l��x=��3�ϣ���PBQ�ܷ��Ϊ�Ե�PΪֱ�Ƕ���ĵ���ֱ�������Σ����ܣ�������������ĵ�P�����ꣻ�����ܣ���˵�����ɣ�

���𰸡���1��![]() ����2��2��h��4����3��P��1��4������0��3������
����2��2��h��4����3��P��1��4������0��3������![]() ��
��![]() ������
������![]() ��
��![]() ����
����
��������
�����������1�����ô���ϵ������������ߵĽ���ʽ���ɣ�
��2�������ֱ��BC����ʽΪy=��x+3������������߶������꣬�ó���x=1ʱ��y=2����������߶��������ɵó������
��3����P��m��![]() ����Q����3��n������3����P��m��
����Q����3��n������3����P��m��![]() ����Q����3��n����������������ۣ��ٵ�P����x���Ϸ�ʱ����P����PM��ֱ��y�ᣬ��y����M�㣬��B����BN��ֱ��MP���ӳ�����N�㣬��֤����PQM�ա�BPN��AAS�����õ�PM=BN����PM=BN=
����Q����3��n����������������ۣ��ٵ�P����x���Ϸ�ʱ����P����PM��ֱ��y�ᣬ��y����M�㣬��B����BN��ֱ��MP���ӳ�����N�㣬��֤����PQM�ա�BPN��AAS�����õ�PM=BN����PM=BN=![]() ������B������ɵ�PN=3��m����PM+PN=6���õ�
������B������ɵ�PN=3��m����PM+PN=6���õ�![]() �������̼�����
�������̼�����
�ڵ�P����x���·�ʱ����P����PM��ֱ��l��M�㣬��B����BN��ֱ��MP���ӳ�����N�㣬ͬ���ɵ���PQM�ա�BPN���õ�PM=BN�� PM=6����3��m��=3+m��BN=![]() ����
����![]() ���ⷽ�̼�����
���ⷽ�̼�����
�����������1���������ߵĶԳ���x=1��B��3��0������A����1��0����
��������![]() ����C��0��3��������x=0ʱ��c=3��
����C��0��3��������x=0ʱ��c=3��
����������![]() ����A����1��0����B��3��0������
����A����1��0����B��3��0������![]() ����
����![]() ���������ߵĽ���ʽΪ��
���������ߵĽ���ʽΪ��![]() ��
��
��2����C��0��3����B��3��0������ֱ��BC����ʽΪy=��x+3����![]() =
=![]() ��������������1��4��
��������������1��4��
������ֱ��BC��y=��x+1����x=1ʱ��y=2����������L����ƽ��h����λ���ȣ�����h=2ʱ�������߶�������BC�ϣ�
��h=4ʱ�������߶�������OB�ϣ�����������L����ƽ��h����λ���ȣ�ʹƽ�ƺ����������ߵĶ���������OBC�ڣ�������OBC�ı߽磩����2��h��4��
��3����P��m��![]() ����Q����3��n����������������ۣ�
����Q����3��n����������������ۣ�
�ٵ�P����x���Ϸ�ʱ����P����PM��ֱ��y�ᣬ��y����M�㣬��B����BN��ֱ��MP���ӳ�����N�㣬��ͼ��ʾ����B��3��0�����ߡ�PBQ���Ե�PΪֱ�Ƕ���ĵ���ֱ�������Σ����BPQ=90�㣬BP=PQ������PMQ=��BNP=90�㣬��MPQ=��NBP������PQM����BPN�У��ߡ�PMQ=��BNP����MPQ=��BNP��PQ=BP�����PQM�ա�BPN��AAS������PM=BN����PM=BN=![]() ������B������ɵ�PN=3��m����PM+PN=6����
������B������ɵ�PN=3��m����PM+PN=6����![]() ����ã�m=1��m=0����P��1��4����P��0��3����
����ã�m=1��m=0����P��1��4����P��0��3����
�ڵ�P����x���·�ʱ����P����PM��ֱ��l��M�㣬��B����BN��ֱ��MP���ӳ�����N�㣬ͬ���ɵ���PQM�ա�BPN����PM=BN����PM=6����3��m��=3+m��BN=![]() ����
����![]() �����m=
�����m=![]() ��
��![]() ����P��
����P��![]() ��
��![]() ����
����![]() ��
��![]() ����
����
���Ͽɵã����������ĵ�P�������ǣ�1��4������0��3������![]() ��
��![]() ���ͣ�
���ͣ�![]() ��
��![]() ����
����
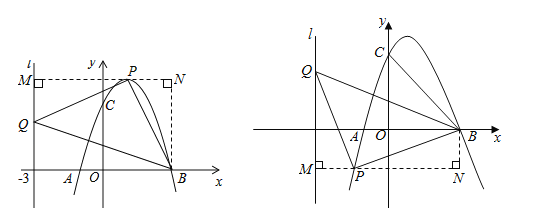



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һˮ���������㡢���㡢���㹲2 000β��С��ͨ����β������飬�������㡢����ĸ�����51%��26%����ˮ������_____β���㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC����BC����ƽ�ƣ���ͼ��B��C�غϣ�C��D�غϣ�A��E�غϣ���֪��ABC�����Ϊ3�����ABCƽ�ƹ�����ɨ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ��2016���ݣ���ͼ1��������![]() �Ķ�������Ϊ��0����1�����Ҿ�����A����2��0����
�Ķ�������Ϊ��0����1�����Ҿ�����A����2��0����

��1���������ߵĽ���ʽ��
��2������������![]() ����x���·���ͼ����x�ᷭ�۵�x���Ϸ���x���Ϸ���ͼ�ֲ��䣬�͵õ��˺���
����x���·���ͼ����x�ᷭ�۵�x���Ϸ���x���Ϸ���ͼ�ֲ��䣬�͵õ��˺���![]() ͼ���ϵ�����һ�㣬ֱ��l�Ǿ�����0��1����ƽ����x���ֱ�ߣ�����P��ֱ��l�Ĵ��ߣ�����ΪD�����벢̽����PO��PD�IJ��Ƿ�Ϊ��ֵ������ǣ�������˶�ֵ��������ǣ���˵�����ɣ�
ͼ���ϵ�����һ�㣬ֱ��l�Ǿ�����0��1����ƽ����x���ֱ�ߣ�����P��ֱ��l�Ĵ��ߣ�����ΪD�����벢̽����PO��PD�IJ��Ƿ�Ϊ��ֵ������ǣ�������˶�ֵ��������ǣ���˵�����ɣ�
��ע���ڽ�������У��������������ѣ������Ķ�����IJ��ϣ�
���Ķ����ϣ�
1����ƽ��ֱ������ϵ�У���A��B���������ֱ�ΪA��![]() ��
��![]() ����B��
����B��![]() ��
��![]() ������A��B�����ľ���Ϊ|AB|=
������A��B�����ľ���Ϊ|AB|=![]() �������ʽ���������빫ʽ��
�������ʽ���������빫ʽ��
���磺��֪A��B���������ֱ�Ϊ����1��2������2����2������A��B�����ľ���Ϊ|AB|=![]() =5��
=5��
2����ʽ�ֽ⣺![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB=12cm��BC=6cm����P��AB�ߴӵ�A��ʼ���B��2cm/����ٶ��ƶ�����Q��DA�ߴӵ�D��ʼ���A��1cm/����ٶ��ƶ������P��Qͬʱ��������t���룩��ʾ�ƶ���ʱ�䣨0��t��6���� 
��1����tΪ��ֵʱ����PBCΪ����ֱ�������Σ�
��2�����ƶ�����QAPΪ����ֱ��������ʱб��QP�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������A���ʾԭ����߾���ԭ��3����λ���ȡ�B����ԭ���ұ߾���ԭ��2����λ���ȣ���ô��������ʾ���������ĺ���10�IJ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����д��һ��һԪһ�β���ʽ��ʹ���Ľ⼯Ϊx��2����ô�������ʽ������________��δ֪����ϵ������Ϊ1����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�κ���y=��k��2��x�� ![]() �У�y��x�������������k�Ŀ���ֵΪ�� ��
�У�y��x�������������k�Ŀ���ֵΪ�� ��
A.1
B.![]()
C.2
D.4
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com