
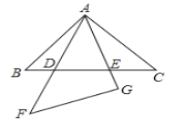
【题目】将两个全等的等腰直角三角形摆成如图所示的样子(图中的所有点,线都在同一平面内),请在图中找出一组相似的三角形,并说明它们相似的理由.
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线![]() 与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.
与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.
(1)求该抛物线的解析式;
(2)如图①,若点D是抛物线上一动点,设点D的横坐标为m(0<m<3),连接CD,BD,BC,AC,当△BCD的面积等于△AOC面积的2倍时,求m的值;
(3)若点N为抛物线对称轴上一点,请在图②中探究抛物线上是否存在点M,使得以B,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点M的坐标;若不存在,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解本校中考体育备考情况,随机抽去九年级部分学生进行了一次测试(满分60分,成绩均记为整数分)并按测试成绩(单位:分)分成四类:A类(54≤a≤60),B类(48≤a≤53),C类(36≤a≤47),D类(a≤35)绘制出如下两幅不完整的统计图,请根据图中信息,解答下列问题:
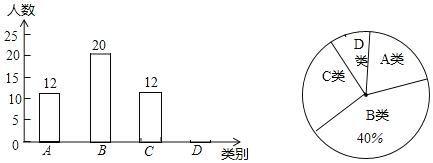
(1)请补全统计图;
(2)在扇形统计图汇总,表示成绩类别为“C”的扇形所对应的圆心角是__°;
(3)该校准备召开体育考经验交流会,已知A类学生中有4人满分(男生女生各有2人),现计划从这4人中随机选出2名学生进行经验介绍,请用树状图或列表法求所抽到的2,名学生恰好是一男一女的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
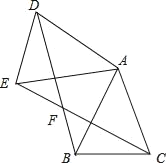
(1)求证:△AEC≌△ADB;(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如右图,正方形ABCD的边长为2,点E是BC边上一点,以AB为直径在正方形内作半圆
O,将△DCE沿DE翻折,点C刚好落在半圆O的点F处,则CE的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:(保留作图痕迹,不写做法)
(1)已知:如图,四边形ABCD与四边形EFGH成中心对称,试画出它们的对称中心O。
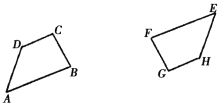
(2)考古学家在考古过程中发现一个圆盘,但是因为历史悠久,已经有一部分缺失,如图所示.现希望复原圆盘,需要先找到圆盘的圆心,才能继续完成后续修复工作.请利用直尺(无刻度)和圆规,在图中找出圆心O.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种流感病毒,有一人患了这种流感,在每轮传染中一人将平均传给x人:
(1)第一轮后患病的人数为 ;(用含x的代数式表示)
(2)在进入第二轮传染之前,有两位患者被及时隔离并治愈,问第二轮传染后总共是否会有21人患病的情况发生,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com