
【题目】如图,在平面直角坐标系中,四边形OABC 的边OC 、OA 分别与 x 轴、 y 轴重合, AOC 90,BCO 45, AB // OC , BC 6 ![]() ,点C 的坐标为 9,0.
,点C 的坐标为 9,0.
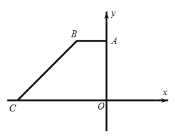

(1)求点 B 的坐标;
(2)若直线 DE 交四边形的对角线 BO 于点 D ,交 y 轴于点 E ,且OE 2 , OD 2BD ,求:
① ODE 的面积;
②点 D 的坐标.
(3)在(2)的条件下,坐标平面内是否存在点 P ,使以O 、E 、P 、D 为顶点的四边形是平行四边形? 若存在,请直接写出点 P 的坐标;若不存在,请说明理由.
【答案】(1)B(﹣3,6);(2)①S△ODE=2,②D(﹣2,4);(3)存在,P点坐标为(﹣2,6),(﹣2,2)或(2,﹣4).
【解析】
(1)过B点作BF⊥OC于点F,根据等腰直角三角形得到性质求得BF,CF的长即可得到B点坐标;
(2)过点D作DG⊥y轴于点G,根据相似三角形的性质可得DG与OG的长,即可得D点坐标,再利用三角形的面积公式求得△ODE的面积即可;
(3)分别以DE,OD,OE为对角线作平行四边形,分情况进行讨论即可.
(1)过点B作BF⊥x轴于F,
在Rt△BCF中,
∵∠BCO=45°,BC=6![]() ,
,
∴CF=BF=6,
∵C 的坐标为(﹣9,0),
∴AB=OF=3,
∴点B的坐标为(﹣3,6);
(2)过点D作DG⊥y轴于点G,
∵AB∥DG,
∴△ABO∽△GDO,
∴![]() ,
,
∵OD 2BD,AB=3,AO=6,
∴DG=2,OG=4,
∴S△ODE=![]() ,
,
点D坐标为:(﹣2,4);
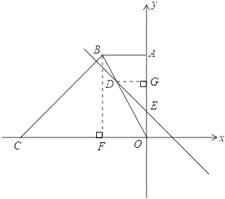
(3)存在,如图2
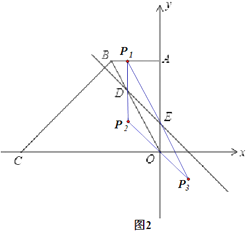
①平行四边形OEP1D,此时DE为对角线,
∴DP1∥OE,DP1=OE=2,
则P1(﹣2,6);
②平行四边形OEP2D,此时DO为对角线,
∴DP2∥OE,DP2=OE=2,
则P2(﹣2,2);
③平行四边形OEP3D,此时OE为对角线,
∴OP3∥DE,OP3=DE,
则P3(2,﹣4);
综上当P点坐标为(﹣2,6),(﹣2,2)或(2,﹣4)时,O、E、P、D为顶点的四边形是平行四边形.


科目:初中数学 来源: 题型:
【题目】如图,海中有一小岛P,在距小岛P的![]() 海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?
海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有三个点A、B、C,完成系列问题:
![]()
(1)A、C两点间的距离是多少?
(2)在数轴上找到点D,使点D到B、C两点的距离相等;并在数轴上标出点D表示的数.
(3)若点E与B点的距离是5,求点E表示的数是什么?
(4)若点F与A点的距离是a(a>0),直接写出点F表示的数是多少?(用字母a表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD和正方形CEFG如图1所示,其中B、C、E在一条直线上,O是AF的中点,连接OD、OG
(1)探究OD与OG的位置关系![]() 的值;(写出结论不用证明)
的值;(写出结论不用证明)
(2)如图2所示,将正方形ABCD和正方形CEFG改为菱形ABCD和菱形CEFG,且∠ABC=∠DCE=120°,探究OD与OG的位置关系,及![]() 的比值;
的比值;
(3)拓展探索:把图1中的正方形CEFG绕C顺时针旋转小于90°的角后,其他条件均不变,问第1问中的两个结论是否发生变化?(写出结论不用证明)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 的意义是数轴上表示x、y 的两点之间的距离。例如:
的意义是数轴上表示x、y 的两点之间的距离。例如:![]() 表示4与 —2 的差的绝对值,实际上也可以理解为 4 与—2 两数在数轴上所对应的两点之间的距离;同理
表示4与 —2 的差的绝对值,实际上也可以理解为 4 与—2 两数在数轴上所对应的两点之间的距离;同理![]() 也可以理解为 x 与 3 两数在数轴上所对应的两点之间的距离。试探索:
也可以理解为 x 与 3 两数在数轴上所对应的两点之间的距离。试探索:
(1)![]() = ;
= ;
(2)若![]() ,则 x= ;
,则 x= ;
(3)请你找出符合条件的整数x ,使得![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
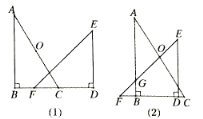
【题目】如图,为一副重叠放置的三角板,其中∠ABC=∠EDF=90°,BC与DF共线,将△DEF沿CB方向平移,当EF经过AC的中点O时,直线EF交AB于点G,若BC=3,则此时OG的长度为( )
A. 3B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市旅游景区有A,B,C,D,E等著名景点,该市旅游部门统计绘制出2018年春节期间旅游情况统计图(如图),根据图中信息解答下列问题:
(1)2018年春节期间,该市A,B,C,D,E这五个景点共接待游客 万人,扇形统计图中E景点所对应的圆心角的度数是 ,并补全条形统计图.
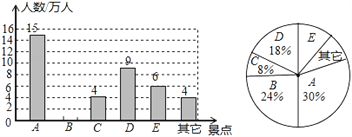
(2)甲,乙两个旅行团在A,B,D三个景点中随机选择一个,这两个旅行团选中同一景点的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是一个长为2m,宽为2n的长方形(m>n),沿图中虚线用剪刀均匀分民四块小长方形,然后按图②的形状拼成一个正方形.

(1)图②中阴影部分的正方形的边长是多少?(用代数式表示)
(2)观察图②写出下列三个代数式:(m+n)2 , (m﹣n)2 , mn之间的等量关系.
(3)若m+n=7,mn=6,求m-n.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(-1,0)和点B(1,2),在![]() 轴上确定点P,使得△ABP为直角三角形,则满足这样条件的点P的坐标是____________________.
轴上确定点P,使得△ABP为直角三角形,则满足这样条件的点P的坐标是____________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com