
如图,四边形ABCD中,AB∥CD,AB∥CD,AD∥BC,AC和BD交于点O.
求证:OA=OC.


【考点】全等三角形的判定与性质.
【专题】证明题.
【分析】由平行线的性质得出∠ABD=∠CDB,∠ADB=∠CBD,由ASA证明△ABD≌△CDB,得出对应边相等AD=CB,再由AAS证明△AOD≌△COB,得出对应边相等即可.
【解答】证明:∵AB∥CD,AD∥BC,
∴∠ABD=∠CDB,∠ADB=∠CBD,
在△ABD和△CDB中,
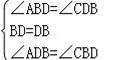
 ,
,
∴△ABD≌△CDB(ASA),
∴AD=CB,
在△AOD和△COB中,
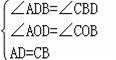
 ,
,
∴△AOD≌△COB(AAS),
∴OA=OC.
【点评】本题考查了平行线的性质、全等三角形的判定与性质;熟练掌握平行线的性质,证明三角形全等是解决问题的关键.


科目:初中数学 来源: 题型:
PM2.5颗粒为小于或等于0.0000025米的微粒,直径虽小,但活性强,易附带有毒、有害物质,且在大气中的停留时间长、输送距离远,因而对人体健康和大气环境质量的影响更大.0.0000025这个数字用科学记数法表示为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
)观察下列等式
①1×3=22﹣1 ②2×4=32﹣1 ③3×5=42﹣1
请你按照三个等式的规律写出第④个,第⑤个算式,并把这个规律用含字母n(n为正整数)的式子表示出来,说明其正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
.阅读与思考:整式乘法与因式分解是方向相反的变形,由(x+p)(x+q)=x2+(p+q)x+pq得,x2+(p+q)x+pq=(x+p)(x+q);利用这个式子可以将某些二次项系数是1的二次三项式分解因式,例如:将式子x2﹣x﹣6分解因式.这个式子的常数项﹣6=2×(﹣3),一次项系数﹣1=2+(﹣3),这个过程可用十字相乘的形式形象地表示:先分解常数项,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项系数.如图所示.这种分解二次三项式的方法叫“十字相乘法”,请同学们认真观察,分析理解后,解答下列问题.
(1)分解因式:x2+7x﹣18.
(2)填空:若x2+px﹣8可分解为两个一次因式的积,则整数p的所有可能值是 .
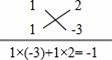

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com