
分析 (1)求工效,时间明显,一定是根据工作总量来列等量关系的.等量关系为:甲6天的工作总量+乙6天的工作总量=1;
(2)让2000×各自的工作量即可.
解答 解:(1)设甲队单独完成此项工程需x天,
由题意得$\frac{6}{x}$+$\frac{6}{\frac{2x}{3}}$=1,
解得x=15,
经检验,x=15是原方程的解.
答:甲队单独完成此项工程需15天,乙队单独完成此项工程需15×$\frac{2}{3}$=10(天).
(2)甲队所得报酬:2000×$\frac{1}{15}$×6=800(元);
乙队所得报酬:2000×$\frac{1}{10}$×6=1200(元).
答:甲队得到800元,乙队得到1200元.
点评 本题考查分式方程的应用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.应用题中一般有三个量,求一个量,明显的有一个量,一定是根据另一量来列等量关系的.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
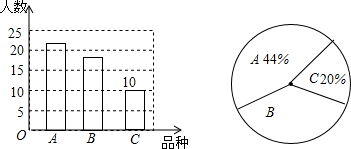
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
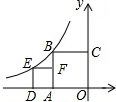 如图,点B,E是反比例函数y=-$\frac{4}{x}$(x<0)图象上的两点,点C在y轴上,点A,D在x轴上,且四边形OABC和四边形ADEF均为正方形,则点D的横坐标是( )
如图,点B,E是反比例函数y=-$\frac{4}{x}$(x<0)图象上的两点,点C在y轴上,点A,D在x轴上,且四边形OABC和四边形ADEF均为正方形,则点D的横坐标是( )| A. | -1-$\sqrt{5}$ | B. | -5+$\sqrt{5}$ | C. | -2$\sqrt{3}$ | D. | -1-2$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
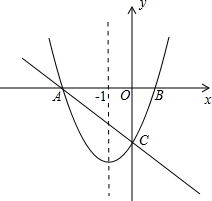 如图,在直角坐标系xOy中,一次函数y=-$\frac{2}{3}$x+m(m为常数)的图象与x轴交于A(-3,0),与y轴交于点C.以直线x=-1为对称轴的抛物线y=ax+bx+c(a,b,c为常数,且a>0)经过A、C两点,与x轴正半轴交于点B.
如图,在直角坐标系xOy中,一次函数y=-$\frac{2}{3}$x+m(m为常数)的图象与x轴交于A(-3,0),与y轴交于点C.以直线x=-1为对称轴的抛物线y=ax+bx+c(a,b,c为常数,且a>0)经过A、C两点,与x轴正半轴交于点B.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
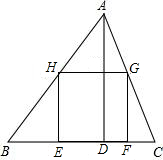 如图,△ABC是一张锐角三角形余料,其中BC=12cm,高AD=6cm,现在要把它剪成一个正方形材料备用,使正方形的一边在BC上,其余两个顶点分别在AB,AC上,则这个正方形材料的边长是多少?
如图,△ABC是一张锐角三角形余料,其中BC=12cm,高AD=6cm,现在要把它剪成一个正方形材料备用,使正方形的一边在BC上,其余两个顶点分别在AB,AC上,则这个正方形材料的边长是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com