
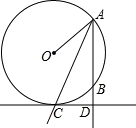
如图,已知OA是圆O的半径,点B在圆O上,∠OAB的平分线AC交圆O于点C,CD⊥AB于点D,求证:CD是圆O的切线.
 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
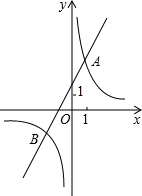
已知反比例函数y1=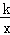 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点(m,﹣2),则满足y1>y2的自变量x的取值范围是__________.
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点(m,﹣2),则满足y1>y2的自变量x的取值范围是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知二次函数y=ax2+bx+c的图象经过A(1,0),B(3,0),C(0,﹣3)
(1)求此二次函数的解析式以及顶点D的坐标;
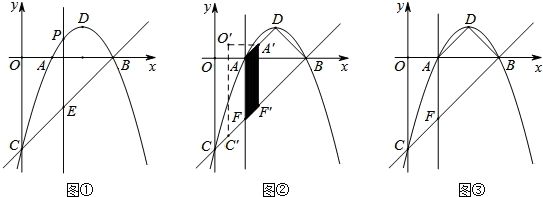
(2)如图①,过此二次函数抛物线图象上一动点P(m,n)(0<m<3)作y轴平行线,交直线BC于点E,是否存在一点P,使线段PE的长最大?若存在,求出PE长的最大值;若不存在,说明理由.
(3)如图②,过点A作y轴的平行线交直线BC于点F,连接DA、DB、四边形OAFC沿射线CB方向运动,速度为每秒1个单位长度,运动时间为t秒,当点C与点F重合时立即停止运动,求运动过程中四边形OAFC与四边形ADBF重叠部分面积S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
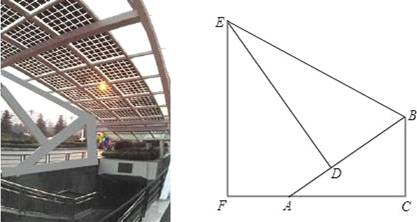
如图是某地下商业街的入口,数学课外兴趣小组的同学打算运用所学的知识测量侧面支架的最高点E到地面的距离EF.经测量,支架的立柱BC与地面垂直,即∠BCA=90°,且BC=1.5m,点F、A、C在同一条水平线上,斜杆AB与水平线AC的夹角∠BAC=30°,支撑杆DE⊥AB于点D,该支架的边BE与AB的夹角∠EBD=60°,又测得AD=1m.请你求出该支架的边BE及顶端E到地面的距离EF的长度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com