
已知反比例函数y1=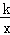 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点(m,﹣2),则满足y1>y2的自变量x的取值范围是__________.
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点(m,﹣2),则满足y1>y2的自变量x的取值范围是__________.
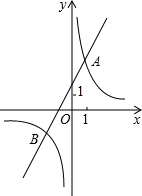
x<﹣2或0<x<1.
【考点】反比例函数与一次函数的交点问题.
【分析】将A坐标代入反比例函数解析式中求出k的值,确定出反比例解析式,将B坐标代入反比例解析式中求出m的值,确定出B坐标,将A与B坐标代入一次函数解析式中求出a与b的值,即可确定出一次函数解析式,利用图象即可得出所求不等式的解集,即为x的范围.
【解答】解:(1)∵函数y1=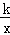 的图象过点A(1,4),即4=
的图象过点A(1,4),即4=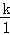 ,
,
∴k=4,
∴反比例函数的关系式为y1=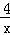 ;
;
又∵点B(m,﹣2)在y1=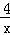 上,
上,
∴m=﹣2,
∴B(﹣2,﹣2),
根据图象y1>y2成立的自变量x的取值范围为x<﹣2或0<x<1.
故答案为:x<﹣2或0<x<1.
【点评】此题考查了一次函数与反比例函数的交点问题,涉及的知识有:待定系数法求函数解析式,利用了数形结合的思想,熟练运用待定系数法是解本题的关键.


科目:初中数学 来源: 题型:
将抛物线y=4x2先向右平移2个单位,再向下平移1个单位,得到的抛物线解析式为( )
A.y=4(x+2)2﹣1 B.y=4(x﹣2)2﹣1 C.y=4(x+2)2+1 D.y=4(x﹣2)2+1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com