
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,反比例函数
,反比例函数![]() (
(![]() )的图像与矩形两边AB、BC分别交于点D、点E,且
)的图像与矩形两边AB、BC分别交于点D、点E,且![]() .
.
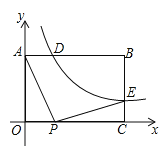
(1)求点D的坐标和![]() 的值;
的值;
(2)求证:![]() ;
;
(3)若点![]() 是线段
是线段![]() 上的一个动点,是否存在点
上的一个动点,是否存在点![]() ,使
,使![]() ?若存在,求出此时点
?若存在,求出此时点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ,4;(2)见解析;(3)存在点
,4;(2)见解析;(3)存在点![]() ,
,![]() 或
或![]() .
.
【解析】
(1)由矩形OABC中,AB=4,BD=2AD,可得3AD=4,即可求得AD的长,然后求得点D的坐标,即可求得k的值,继而求得点E的坐标;
(2)由E点在反比例函数![]() 图像上,可求E点坐标,进而求出EC的长即可求证.
图像上,可求E点坐标,进而求出EC的长即可求证.
(3)首先假设存在要求的点P坐标为(m,0),OP=m,CP=4-m,由∠APE=90°,易证得△AOP∽△PCE,然后由相似三角形的对应边成比例,求得m的值,继而求得此时点P的坐标.
解:(1)在矩形![]() 中,
中,![]() 轴,且
轴,且![]() ,
,

∴点![]() 的纵坐标为3.
的纵坐标为3.
∵![]() ,且
,且![]() ,
,
![]() ,
,
∴![]() .
.
∴点![]() 在反比例函数
在反比例函数![]() 图像上,
图像上,
∴![]() .
.
(2)证:∵![]() 在
在![]() 上,
上,
∴![]() 横坐标为4,
横坐标为4,
在![]() 中,当
中,当![]() 时,
时,![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(3)存在点![]() ,使
,使![]() ,其过程是:
,其过程是:
设![]() ,则
,则![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() ,即
,即![]() .解得
.解得![]() 或
或![]() .
.
![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,给出如下定义:已知两个函数,如果对于任意的自变量![]() ,这两个函数对应的函数值记为
,这两个函数对应的函数值记为![]() , 恒有点
, 恒有点![]() 和点
和点![]() 关于点
关于点![]() 成中心对称(此三个点可以重合),由于对称中心
成中心对称(此三个点可以重合),由于对称中心![]() 都在直线
都在直线![]() 上,所以称这两个函数为关于直线
上,所以称这两个函数为关于直线![]() 的“相依函数”。例如:
的“相依函数”。例如: ![]() 和
和![]() 为关于直线
为关于直线![]() 的 “相依函数”.
的 “相依函数”.
(1)已知点![]() 是直线
是直线![]() 上一点,请求出点
上一点,请求出点![]() 关于点
关于点![]() 成中心对称的点
成中心对称的点![]() 的坐标:
的坐标:
(2)若直线![]() 和它关于直线
和它关于直线![]() 的“相依函数”的图象与
的“相依函数”的图象与![]() 轴围成的三角形的面积为
轴围成的三角形的面积为![]() ,求
,求![]() 的值;
的值;
(3)若二次函数![]() 和
和![]() 为关于直线
为关于直线![]() 的“相依函数”.
的“相依函数”.
①请求出![]() 的值;
的值;
②已知点![]() 、点
、点![]() 连接
连接![]() 直接写出
直接写出![]() 和
和![]() 两条抛物线与线段
两条抛物线与线段![]() 有目只有两个交占时对应的
有目只有两个交占时对应的![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c交x轴于A(﹣1,0),B(3,0),交y轴的负半轴于C,顶点为D.下列结论:①2a+b=0;②2c<3b;③当m≠1时,a+b<am2+bm;④当△ABD是等腰直角三角形时,则a=![]() ;⑤当△ABC是等腰三角形时,a的值有3个.其中正确的有( )个.
;⑤当△ABC是等腰三角形时,a的值有3个.其中正确的有( )个.

A. 5 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“食品安全”受到全社会的广泛关注,育才中学对部分学生就食品安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面的两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
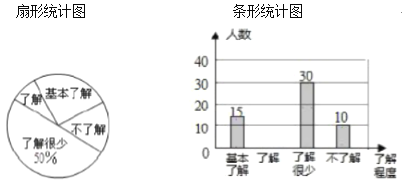
(1)接受问卷调查的学生共有________人,扇形统计图中“基本了解”部分所对应扇形的圆心角为_________![]() ;
;
(2)请补全条形统计图;
(3)若对食品安全知识达到“了解”程度的学生中,男、女生的比例恰为![]() ,现从中随机抽取
,现从中随机抽取![]() 人参加食品安全知识竞赛,则恰好抽到
人参加食品安全知识竞赛,则恰好抽到![]() 个男生和
个男生和![]() 个女生的概率________.
个女生的概率________.
查看答案和解析>>
科目:初中数学 来源: 题型:
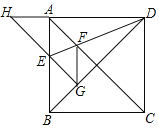
【题目】如图,正方形ABCD的边长为1,AC、BD是对角线,将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:①四边形AEGF是菱形;②△HED的面积是1﹣![]() ;③∠AFG=135°;④BC+FG=
;③∠AFG=135°;④BC+FG=![]() .其中正确的结论是_____.(填入正确的序号)
.其中正确的结论是_____.(填入正确的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A点的坐标为(﹣1,5),B点的坐标为(3,3),C点的坐标为(5,3),D点的坐 标为(3,﹣1),小明发现:线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC是等腰直角三角形,∠BAC= 90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.

(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长DB交CF于点H.
①求证:BD⊥CF;
②当AB=2,AD=3![]() 时,求线段DH的长.
时,求线段DH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上,另一个顶
点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图(3),
则三角板的最大边的长为( )
A. ![]() B.
B. ![]() C.
C.![]()
![]() D.
D. ![]()
![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
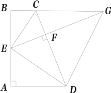
【题目】如图,已知四边形ABCD中,AB⊥AD,BC∥AD,E为AB的中点,且EC、ED分别为∠BCD、∠ADC的角平分线,EF⊥CD交BC的延长线于点G,连接DG.
(1)求证:CE⊥DE;
(2)若AB=6,求CF·DF的值;
(3)当△BCE与△DFG相似时,![]() 的值是 .
的值是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com