
【题目】平面直角坐标系中,点A的坐标为(2,4),点B的坐标为(2,7) ,直线l经过A点且平行于x
轴,直线l上的动点C从A点出发以每秒4个单位的速度沿直线l运动.若在x轴上有两点D、E,
连接DB、OB,连接EC、OC,满足DB=OB,EC=OC,设点C运动时间t秒,
(1) 如图1,若动点C从A点出发向左运动,当t=1秒时,
①求线段BC的长和点E的坐标;
②求此时DE与AC的数量关系?
(2)探究:动点C在直线l运动,无论t取何值,是否都存在上述(1)②中的数量关系? 若存在,请证明;若不存在,请说明理由.


图1 图2
【答案】(1) ①BC=5, E(-4,0)②DE=2AC (2)存在,证明见解析
【解析】试题分析:(1)①根据题意可知AC=4,AB=3,由勾股定理即可得BC的长,再根据EC=OC以及点C的坐标即可得点E的坐标;
②由点B的坐标以及DB=OB即可得点D的坐标,从而得到DE的长,从而可得;
(2)由题意可知AC=4t,C(2-4t,4),从而可得E(4-8t,0),由D(4,0)可得DE=8t,从而可得.
试题解析:(1)①当t=1时,AC=4t=4,4-2=2,所以C(-2,4),
由A(2,4)、B(2,7)可得AB=3,
由勾股定理则有BC=5,
因为EC=OC,C(-2,4),O(0,0),所以E(-4,0);
②由OB=BD,O(0,0),B(2,7),所以D(4,0),
由E(-4,0),所以DE=8,
因为AC=4,所以DE=2AC;
(2)存在,理由如下:
∵AC=4t,A(2,4),∴C(2-4t,4),
∵EC=OC, O(0,0),∴E(4-8t,0);
∵OB=BD,O(0,0),B(2,7),∴D(4,0),
∴DE=8t,
∴DE=2AC.


科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点分别为A(-2,3),B(-3,2),C(-1,1)
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)请在x轴上确定一点D,使点D到B、C的距离相等(要求用直尺和圆规作图,并保留作图痕迹)
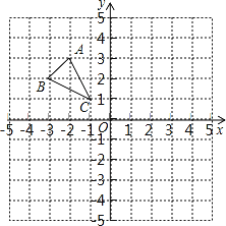
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AC∥DF,直线AF分别直线BD、CE 相交于点G、H,∠1=∠2,
求证:∠C=∠D.

证明: ∵∠1=∠2(已知)
∠1=∠DGH( ),
∴∠2=__________( 等量代换 )
∴__________∥__________( 同位角相等,两直线平行 )
∴∠C=___________( 两直线平行,同位角相等 )
又∵AC∥DF__________
∴∠D=∠ABG_________
∴∠C=∠D__________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,己知OA丄OB, ∠AOC=∠BOD,由此判定OC丄OD,下面是推理过程,请在横线上填空.
![]() OA丄OB(己知)
OA丄OB(己知)
![]() _________=90° (______________)
_________=90° (______________)
![]() ∠AOB=∠AOC-∠BOC, ∠COD=∠BOD-∠BOC
∠AOB=∠AOC-∠BOC, ∠COD=∠BOD-∠BOC
∠AOC=∠BOD
![]() ∠AOB=∠COD (等式的性质)
∠AOB=∠COD (等式的性质)
![]() _________=90°
_________=90°
![]() CO 丄 OD (_____________________)
CO 丄 OD (_____________________)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形ABCD沿着对角线BD折叠,使点C落在C′处,BC′交AD于点E.
(1)若∠DBC=25°,求∠ADC′的度数;
(2)若AB=4,AD=8,求△BDE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.
(1)△ABC的面积为______;
(2)将△ABC经过平移后得到△A′B′C′,图中标出了点B的对应点B′,补全△A′B′C′;
(3)若连接AA′,BB′,则这两条线段之间的关系是______;
(4)在图中画出△ABC的高CD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知长方形ABCD,AB=CD, BC=AD,P为长方形ABCD边上的动点,动点P从A出发,沿着A→B→C→D运动到D点停止,速度为2cm/s,设点P用的时间为x秒,△APD的面积为y![]() ,y和x的关系如图2所示.
,y和x的关系如图2所示.

(1)AB=________cm, BC=______cm;
(2)写出![]() 时,y与x之间的关系式;
时,y与x之间的关系式;
(3)当y=12时,求x的值;
(4)当P在线段BC上运动时,是否存在点P使得△APD的周长最小,若存在,求出此时∠APD的度数,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com