
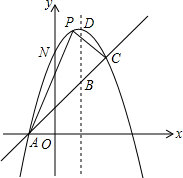
 如图,已知抛物线y=-x2+bx+c过(1,4)与(4,-5)两点,且与一直线y=x+1相交于A,C两点,
如图,已知抛物线y=-x2+bx+c过(1,4)与(4,-5)两点,且与一直线y=x+1相交于A,C两点,分析 (1)由抛物线y=-x2+bx+c过(1,4)与(4,-5)两点,可以求得该抛物线的解析式;
(2)由第一问中抛物线的解析式和直线的解析式连立方程组,即可求得A,C两点的坐标;
(3)作辅助线过点P作PH⊥x轴交AC于点Q,交x轴于点H,过点C作CG⊥x轴交x轴于点G,画出相应的图形,根据已知和第(1)(2)中求出的量进行灵活变化,可以求得△APC的面积,P是抛物线上位于直线AC上方的一个动点,确定点P横坐标的取值范围,从而可以得到△APC的面积的最大值.
解答 解:(1)∵抛物线y=-x2+bx+c过点(1,4)与(4,-5),
∴$\left\{\begin{array}{l}-1+b+c=4\\-16+4b+c=-5\end{array}\right.$,
解得,$\left\{\begin{array}{l}b=2\\ c=3\end{array}\right.$.
∴该抛物线解析式为:y=-x2+2x+3.
(2)∵抛物线y=-x2+2x+3与直线y=x+1相交于A,C两点,
∴x+1=-x2+2x+3.
解得x1=-1,x2=2.
当x=-1时,y=-1+1=0;
当x=2时,y=2+1=3.
∴点A的坐标为;(-1,0),点C的坐标为:(2,3).
(3)如图,过点P作PH⊥x轴交AC于点Q,交x轴于点H,过点C作CG⊥x轴交x轴于点G,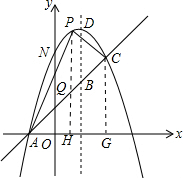
∵点Q在直线y=x+1上,点P在抛物线y=-x2+2x+3上,
∴设Q的坐标为(x,x+1),则P的坐标为(x,-x2+2x+3).
∴PQ=(-x2+2x+3)-(x+1)=-x2+x+2.
∴S△APC=S△PQA+S△PQC=$\frac{PQ×AH}{2}+\frac{PQ×HG}{2}=\frac{PQ×AG}{2}$=$\frac{(-{x}^{2}+x+2)×[2-(-1)]}{2}=\frac{3}{2}(-{x}^{2}+x+2)$=$-\frac{3}{2}(x-\frac{1}{2})^{2}+\frac{27}{8}$.
∵P是抛物线上位于直线AC上方的一个动点,点A的坐标为;(-1,0),点C的坐标为:(2,3),
∴-1<x<3.
∴当$x=\frac{1}{2}$时,△APC的面积取得最大值,最大值为$\frac{27}{8}$.
即P是抛物线上位于直线AC上方的一个动点,△APC的面积的最大值是$\frac{27}{8}$.
点评 本题考查求二次函数的解析式、直线与二次函数的交点问题、求最值的问题,关键是找出所求问题需要的量,灵活变化,最终得出问题的答案.


科目:初中数学 来源: 题型:解答题
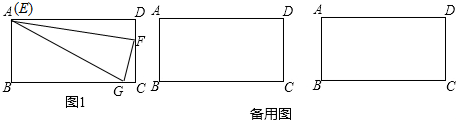
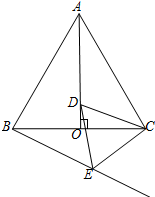 如图,AO是边长为2的等边△ABC的高,点D是AO上的一个动点(点D不与点A、O重合),以CD为一边在AC下方作等边△CDE,连结BE并延长,交AC的延长线于点F.
如图,AO是边长为2的等边△ABC的高,点D是AO上的一个动点(点D不与点A、O重合),以CD为一边在AC下方作等边△CDE,连结BE并延长,交AC的延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,点M在锐角∠AOB的内部,在OA边上求作一点P,在OB边上求作一点Q,使得MP+PQ最小.若OM=2,OM平分∠AOB,并且∠AOB=20°,求这个最小值.
已知:如图,点M在锐角∠AOB的内部,在OA边上求作一点P,在OB边上求作一点Q,使得MP+PQ最小.若OM=2,OM平分∠AOB,并且∠AOB=20°,求这个最小值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
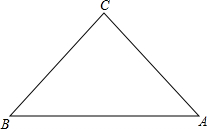 已知:如图,在△ABC中,AC=BC=5,AB=6,请以点A为原点,以AB所在的直线为x轴建立平面直角坐标系,并求出△ABC的各顶点坐标.
已知:如图,在△ABC中,AC=BC=5,AB=6,请以点A为原点,以AB所在的直线为x轴建立平面直角坐标系,并求出△ABC的各顶点坐标.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com