
分析 根据题意假设出甲、乙两地距离以及时速,进而利用时间差值得出等式,进而求出答案.
解答 解:设甲、乙两地相距x千米,计划时速ykm/h,根据题意可得:
$\frac{x}{(20%+1)y}$+1=$\frac{x}{y}$,
故$\frac{x}{1.2y}$-$\frac{x}{y}$+1=0,
整理得:x-1.2x+1.2y=0,
则-2x+12y=0,
故y=$\frac{1}{6}$x,
$\frac{x-200}{(1+25%)y}$+$\frac{48}{60}$+$\frac{200}{y}$=$\frac{x}{y}$,
则$\frac{x-200}{1.25y}$+$\frac{4}{5}$+$\frac{200}{y}$=$\frac{x}{y}$,
代入y=$\frac{1}{6}$x解得:x=600,
检验得:x=600是原方程的根,
答:甲、乙两地相距600千米.
点评 此题主要考查了分式方程的应用,正确得出两地距离与时速的差值是解题关键.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:初中数学 来源: 题型:解答题
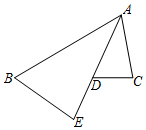 如图,已知AE 平分∠BAC,$\frac{AB}{AE}$=$\frac{AD}{AC}$.
如图,已知AE 平分∠BAC,$\frac{AB}{AE}$=$\frac{AD}{AC}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
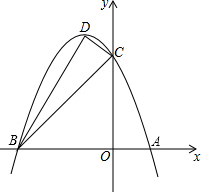 如图,抛物线y=ax2+bx+c的对称轴为x=-1,该抛物线与x轴交于A、B两点,且A点坐标为(1,0),交y轴于C(0,3),设抛物线的顶点为D.
如图,抛物线y=ax2+bx+c的对称轴为x=-1,该抛物线与x轴交于A、B两点,且A点坐标为(1,0),交y轴于C(0,3),设抛物线的顶点为D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2×105 | B. | 20×104 | C. | 0.2×106 | D. | 2×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处.分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系,抛物线y=ax2+bx+c经过O,D,C三点.
如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处.分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系,抛物线y=ax2+bx+c经过O,D,C三点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,点C在线段AB上,点M、N分别是AC、BC的中点.
已知:如图,点C在线段AB上,点M、N分别是AC、BC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com