Question

16．如图，在Rt△AOB中，∠AOB=90°，OA=3．，OB=4，点C从O点出发沿射线OA以每秒1个单位长度的速度匀速运动，同时点D从A点出发沿AB以每秒1个单位长度的速度向B点匀速运动，当点D到达B时C、D都停止运动，点E是CD的中点，过点E作CD的垂线交直线OB于点F，点E′与点E关于OB对称，EE′交直线OB于点G，设点C、D的运动时间为t（秒），
（1）当t=1时，AC=2，点D到OB的距离为$\frac{12}{5}$
（2）当EF与△AOB的一边垂直时，求t的值；
（3）求△EFE′为等腰直角三角形时，t的值；
（4）求当△ADC为等腰三角形时EE′的长度．

Answer 1

分析 （1）如图1，作点D到OB的距离DH，先根据时间和速度表示出两动点C和D的路程OC和AD的长，并将t=1代入，根据平行线分线段成比例定理求DH的长；
（2）分两种情况：①当EF⊥OB时，如图2，根据同角的三角函数列式求时间t的值；
②如图3，当点C与A重合时，EF⊥AB，此时t=3；
（3）（3）分两种情况：
①如图4，当∠FEE′=45°时，△EFE′为等腰直角三角形，证明△DCM是等腰直角三角形，根据DM=CM列方程求出t的值即可，
②如图5，当∠FEE′=45°时，△EFE′为等腰直角三角形，根据CH=DH列方程求出t的值；
（4）分三种情况讨论：
①当AC=CD时，如图6，②当AC=AD时，如图7，③当AD=CD时，如图8，先求t的值，再根据三角函数求EE′的长．

解答 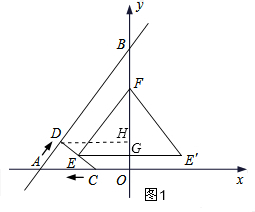解：（1）如图1，过D作DH⊥OB于H，
∵∠AOB=90°，OA=3．，OB=4，
∴AB=$\sqrt{{3}^{2}+{4}^{2}}$=5，
当t=1时，OC=t=1，AD=t=1，
∴AC=OA-OC=3-1=2，
BD=AB-AD=5-1=4，
∵DH∥OA，
∴$\frac{DH}{AO}=\frac{BD}{AB}$，
∴$\frac{DH}{3}=\frac{4}{5}$，
∴DH=$\frac{12}{5}$，
故答案为：2，$\frac{12}{5}$；
（2）分两种情况：
①当EF⊥OB时，如图2，则∠EFO=90°，
∵EF⊥CD，
∴∠CEF=90°，
∵∠AOB=90°，
∴四边形ECOF为矩形，
∴∠ECO=90°，
∴∠ACD=90°，
cos∠BAO=$\frac{OA}{BA}$=$\frac{AC}{AD}$，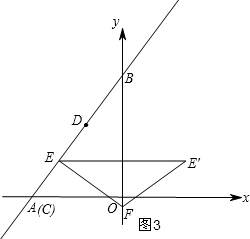
∴$\frac{3}{5}=\frac{3-t}{t}$，
∴t=$\frac{15}{8}$；
②如图3，当点C与A重合时，EF⊥AB，
此时t=3，
∴当EF与△AOB的一边垂直时，t的值为$\frac{15}{8}$或3；
（3）分两种情况：
①如图4，当∠FEE′=45°时，△EFE′为等腰直角三角形，
过D作DM⊥OA于M，
∵sin∠BAO=$\frac{DM}{t}=\frac{4}{5}$，cos∠BAO=$\frac{AM}{t}=\frac{3}{5}$，
∴DM=$\frac{4}{5}$t，AM=$\frac{3}{5}$t，
∴MC=OA-OC-AM=3-t-$\frac{3}{5}$t=3-$\frac{8}{5}$t，
∵EE′⊥y轴，x轴⊥y轴，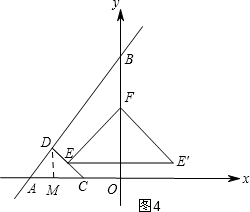
∴EE′∥x轴，
∴∠E′EC=∠ACD，
∵CD⊥EF，
∴∠CEF=90°，
∵∠FEE′=45°，
∴∠E′EC=90°-45°=45°，
∴∠ACD=45°，
∴△DCM是等腰直角三角形，
∴DM=CM，
∴$\frac{4}{5}$t=3-$\frac{8}{5}$t，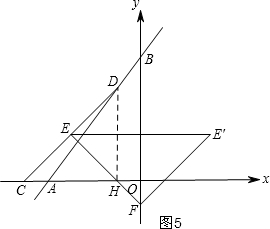
t=$\frac{5}{4}$；
②如图5，当∠FEE′=45°时，△EFE′为等腰直角三角形，
连接OH，
同理得：∠CHE=45°，
∵EF垂直平分CD，
∴CH=DH，∠DHE=∠CHE=45°，
∴∠DHC=90°，
∴DH=$\frac{4}{5}$t，
∵CH=CO-OH=CO-（OA-AH）=t-（3-$\frac{3}{5}$t），
则t-（3-$\frac{3}{5}$t）=$\frac{4}{5}$t，
t=$\frac{15}{4}$，
∴△EFE′为等腰直角三角形时，t的值为$\frac{5}{4}$或$\frac{15}{4}$；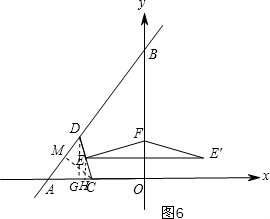
（4）分三种情况讨论：
①当AC=CD时，如图6，
过C作CM⊥AB于M，则AM=DM=$\frac{1}{2}$t，
cos∠BAO=$\frac{AM}{AC}=\frac{AO}{AB}$，
∴$\frac{\frac{1}{2}t}{3-t}=\frac{3}{5}$，
t=$\frac{18}{11}$；
∴OC=$\frac{18}{11}$，
∴AC=3-$\frac{18}{11}$=$\frac{15}{11}$，
∵AG=$\frac{3}{5}$t=$\frac{3}{5}$×$\frac{18}{11}$=$\frac{54}{55}$，
∴CG=AC-AG=$\frac{15}{11}$-$\frac{54}{55}$=$\frac{21}{55}$，
∴HC=$\frac{1}{2}$CG=$\frac{21}{110}$，
∴EE′=2OH=2（OC+CH）=2×（$\frac{18}{11}$+$\frac{21}{110}$）=$\frac{201}{55}$；
②当AC=AD时，如图7，
则t=3-t，
t=$\frac{3}{2}$，
分别过D、E两点作AC的垂线DM、EN，垂足分别为M、N，
AM=$\frac{3}{5}$t=$\frac{3}{5}×\frac{3}{2}$=$\frac{9}{10}$，
∴MC=AC-AM=$\frac{3}{2}$-$\frac{9}{10}$=$\frac{3}{5}$，
∵E是DC的中点，EN∥DM，
∴MN=NC=$\frac{1}{2}$MC=$\frac{3}{5}$×$\frac{1}{2}$=$\frac{3}{10}$，
∴EE′=2ON=2×（OC+NC）=2×（$\frac{3}{2}$+$\frac{3}{10}$）=$\frac{18}{5}$；
③当AD=CD时，如图8，
过D作DM⊥OA于M，
∴AM=CM=$\frac{3}{5}$t，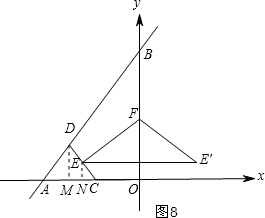
则$\frac{3}{5}$t+$\frac{3}{5}$t+t=3，
t=$\frac{15}{11}$，
∴AD=$\frac{15}{11}$，
∴CE=$\frac{15}{22}$，
过E作EN⊥AC于N，
∵$\frac{CN}{CE}=\frac{3}{5}$，
∴CN=$\frac{15}{22}$，
∴EE′=2ON=2×（OC+NC）=2×（$\frac{15}{11}$+$\frac{9}{22}$）=$\frac{39}{11}$；
综上所述，当△ADC为等腰三角形时EE′的长度为$\frac{201}{55}$或$\frac{18}{5}$或$\frac{39}{11}$．

点评 本题是三角形的综合题，综合性较强，计算量大；考查了一元一次方程、等腰三角形、等腰直角三角形的性质和判定及轴对称的性质，还运用了三角函数表示边长，与方程相结合，求线段的长；本题运用的知识点较多，题目比较好，但难度偏大．