
【题目】等腰直角三角板的一个锐角顶点与正方形ABCD的顶点A重合,两边分别交BC、CD于M、N.
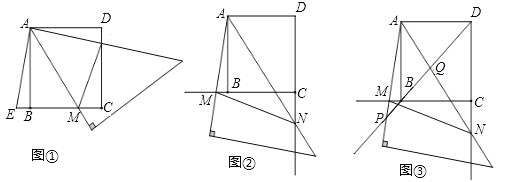
(1)如图①,作AE⊥AN交CB的延长线于E,求证:△ABE≌△AND;
(2)如图②,若M、N分别在边CB、DC所在的直线上时.
①求证:BM+MN=DN;②如图③,作直线BD交直线AM、AN于P、Q两点,若MN=10,CM=8,求AP的长.
【答案】(1)见解析;(2)①见解析;②AP=3![]() .
.
【解析】
(1)利用互余判断出∠EAB=∠NAD,即可得出结论;
(2)先构造出△ADG≌△ABM,进而判断出,△AMG为等腰直角三角形,即可得出NM=NG,即可得出结论;
(3)由(2)得出MN+BM=DN,进而得出CN=18-2BC,再利用勾股定理得求出CN=6,在判断出△ABP∽△ACN,得出![]() ,再利用勾股定理求出AN,代入即可得出结论.
,再利用勾股定理求出AN,代入即可得出结论.
解:(1)如图①,
∵AE垂直于AN,
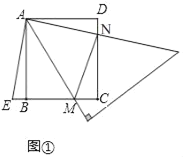
∴∠EAB+∠BAN=90°,
∵四边形ABCD是正方形,
∴∠BAD=90°,
∴∠NAD+∠BAN=90°,
∴∠EAB=∠NAD,
又∵∠ABE=∠D=90°,AB=AD,
∴△ABE≌△AND;………………
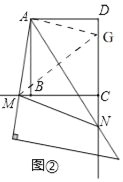
(2)如图②,在ND上截取DG=BM,连接AG、MG,
∵AD=AB,∠ADG=∠ABM=90°,
∴△ADG≌△ABM,
∴AG=AM,∠MAB=∠GAD,
∵∠BAD=∠BAG+∠GAD=90°,
∴∠MAG=∠BAG+∠MAB=90°,
∴△AMG为等腰直角三角形,
∴AN⊥MG,
∴AN为MG的垂直平分线,
∴NM=NG,
∴DN﹣BM=MN,
即MN+BM=DN;
(3)如图③,连接AC,同(2),证得
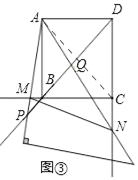
MN+BM=DN,
∴MN+CM﹣BC=DC+CN,
∴CM﹣CN+MN=DC+BC=2BC,
即8﹣CN+10=2BC,
即CN=18﹣2BC,
在Rt△MNC中,
根据勾股定理得MN2=CM2+CN2,即102=82+CN2,
∴CN=6,
∴BC=6,
∴AC=6![]() ,
,
∵∠BAP+∠BAQ=45°,∠NAC+∠BAQ=45°,
∴∠BAP=∠NAC,
又∵∠ABP=∠ACN=135°,
∴△ABP∽△ACN,
∴![]()
在Rt△AND中,
根据勾股定理得AN2=AD2+DN2=36+144,
解得AN=6![]() ,
,
∴![]() ,
,
∴AP=3![]() .
.


科目:初中数学 来源: 题型:
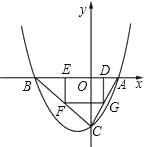
【题目】如图,已知抛物线P:y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F、G分别在线段BC、AC上,抛物线P上部分点的横坐标对应的纵坐标如下:
x | … | ﹣3 | ﹣2 | 1 | 2 | … |
y | … |
| ﹣4 |
| 0 | … |
(1)求A、B、C三点的坐标;
(2)若点D的坐标为(m,0),矩形DEFG的面积为S,求S与m的函数关系,并指出m的取值范围;
(3)当矩形DEFG的面积S取最大值时,连接DF并延长至点M,使FM=kDF,若点M不在抛物线P上,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尺规作图特有的魅力使无数人沉湎其中.传说拿破仑曾通过下列尺规作图将圆等分:
①将半径为r的⊙O六等分,依次得到A,B,C,D,E,F六个分点;
②分别以点A,D为圆心,AC长为半径画弧,两弧相交于点G;
③连接OG,以OG长为半径,从点A开始,在圆周上依次截取,刚好将圆等分.顺次连接这些等分点构成的多边形面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
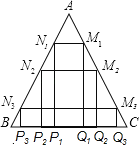
【题目】如图,在△ABC中,AB=AC=![]() ,BC=2.现分别任作△ABC的内接矩形P1Q1M1N1,P2Q2M2N2,P3Q3M3N3,设这三个内接矩形的周长分别为c1、c2,c3,则c1+c2+c3的值是( )
,BC=2.现分别任作△ABC的内接矩形P1Q1M1N1,P2Q2M2N2,P3Q3M3N3,设这三个内接矩形的周长分别为c1、c2,c3,则c1+c2+c3的值是( )
A. 6B. ![]() C. 12D.
C. 12D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
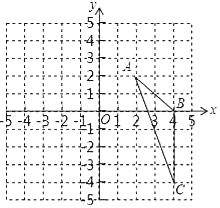
【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4).
(1)请在图中,画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)以点O为位似中心,将△ABC缩小为原来的![]() ,得到△A2B2C2,请在图中y轴右侧,画出△A2B2C2,并求出∠A2C2B2的正弦值.
,得到△A2B2C2,请在图中y轴右侧,画出△A2B2C2,并求出∠A2C2B2的正弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
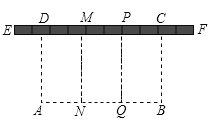
【题目】如图,EF是一面长18米的墙,用总长为32米的木栅栏(图中的虚线)围一个矩形场地ABCD,中间用栅栏隔成同样三块.若要围成的矩形面积为60平方米,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县教育局为了丰富初中学生的大课间活动,要求各学校开展形式多样的阳光体育活动.某中学就“学生体育活动兴趣爱好”的问题,随机调查了本校某班的学生,并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图:
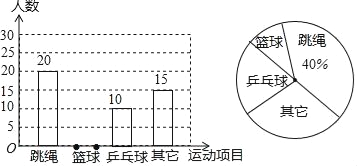
(1)在这次调查中,喜欢篮球项目的同学有 人,在扇形统计图中,“乒乓球”的百分比为 %,如果学校有800名学生,估计全校学生中有 人喜欢篮球项目.
(2)请将条形统计图补充完整.
(3)在被调查的学生中,喜欢篮球的有2名女同学,其余为男同学.现要从中随机抽取2名同学代表班级参加校篮球队,请直接写出所抽取的2名同学恰好是1名女同学和1名男同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华汉字,寓意深广.为了传承中华民族优秀传统文化,我市某中学举行“汉字听写”比赛,赛后整理参赛学生的成绩,将学生的成绩分为A,B,C,D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图,但均不完整.

请你根据统计图解答下列问题:
(1)参加比赛的学生共有____名;
(2)在扇形统计图中,m的值为____,表示“D等级”的扇形的圆心角为____度;
(3)组委会决定从本次比赛获得A等级的学生中,选出2名去参加全市中学生“汉字听写”大赛.已知A等级学生中男生有1名,请用列表法或画树状图法求出所选2名学生恰好是一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角三角形中,如果已知2个元素(其中至少有一个是边),那么就可以求出其余的3个未知元素.对于任意三角形,我们需要知道几个元素就可以求出其余的未知元素呢?思考并解答下列问题:
(1)观察下列4幅图,根据图中已知元素,可以求出其余未知元素的三角形是 .
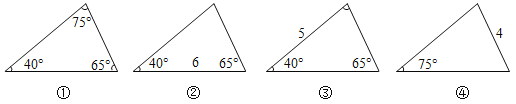
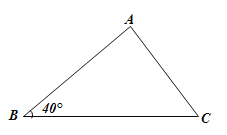
(2)如图,在△ABC中,已知∠B=40°,BC=18,AB=15,请求出AC的长度(答案保留根号).(参考数据:sin40°≈0.6,cos40°≈0.8,tan40°≈0.75)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com