
【题目】尺规作图特有的魅力使无数人沉湎其中.传说拿破仑曾通过下列尺规作图将圆等分:
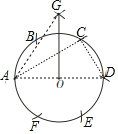
①将半径为r的⊙O六等分,依次得到A,B,C,D,E,F六个分点;
②分别以点A,D为圆心,AC长为半径画弧,两弧相交于点G;
③连接OG,以OG长为半径,从点A开始,在圆周上依次截取,刚好将圆等分.顺次连接这些等分点构成的多边形面积为_____.

【答案】2r2
【解析】
根据作法得到六边形ABCDEF为⊙O的内接正六边形,则有∠CAD=30°,∠ACD=90°,利用特殊角的三角函数值得到CD=r,AC=![]() r,再利用作法得到GO⊥AD,利用勾股定理求得OG=
r,再利用作法得到GO⊥AD,利用勾股定理求得OG=![]() r,然后判断以OG长为半径,从点A 开始,在圆周上依次截取,刚好将圆4等分,顺次连接这些等分点构成了正方形,再利用正方形的面积公式进行计算即可.
r,然后判断以OG长为半径,从点A 开始,在圆周上依次截取,刚好将圆4等分,顺次连接这些等分点构成了正方形,再利用正方形的面积公式进行计算即可.
连接AD、AC、AG,如图,
∵将半径为r的⊙O六等分,依次得到A,B,C,D,E,F六个分点,
∴∠CAD=30°,∠ACD=90°,
∴CD=ADsin30°=r,AC=ADcos30°=![]() r,
r,
∵GA=GD,
∴GO⊥AD,
∴OG=![]() ,
,
以OG长为半径,从点A开始,在圆周上依次截取,刚好将圆4等分,顺次连接这些等分点构成的多边形为正方形,
∴这个多边形面积=![]() r
r![]() r=2r2,
r=2r2,
故答案为:2r2.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
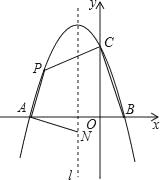
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为x=﹣1.
(1)求抛物线的解析式并写出其顶点坐标;
(2)若动点P在第二象限内的抛物线上,动点N在对称轴l上.
①当PA⊥NA,且PA=NA时,求此时点P的坐标;
②当四边形PABC的面积最大时,求四边形PABC面积的最大值及此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
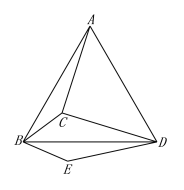
【题目】如图,在△ABC和△DCB中,AB = DC,AC = DB,AC与DB交于点M.

【1】求证:△ABC≌△DCB
【2】过点C作CN∥BD,过点B作BN∥AC,CN与BN交于点N,试判断线段BN与CN的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将![]() 绕点B顺时针旋转
绕点B顺时针旋转![]() ,得到
,得到![]() ,连接
,连接![]() 、
、![]() .
.
(1)求证:![]() 为等边三角形;
为等边三角形;
(2)若![]() ,
,![]() ,
,![]() ,求
,求![]() ;
;
(3)已知![]() ,点
,点![]() 在四边形
在四边形![]() 内部(包括边界).若点F由点B运动至点E,其运动过程满足
内部(包括边界).若点F由点B运动至点E,其运动过程满足![]() ,求点
,求点![]() 运动路径的长.
运动路径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
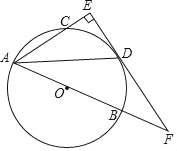
【题目】如图,AB为⊙O的直径,C为⊙O上一点,∠CAB的平分线交⊙O于点D,过点D作ED⊥AE,垂足为E,交AB的延长线于F.
(1)求证:ED是⊙O的切线;
(2)若AD=4![]() ,AB=6,求FD的长.
,AB=6,求FD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
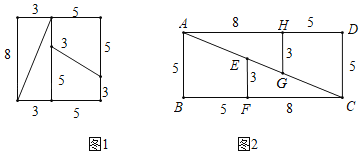
【题目】直觉的误差:有一张8cm×8cm的正方形纸片,面积是64cm2.把这些纸片按图1所示剪开成四小块,其中两块是三角形,另外两块是梯形.把剪出的4个小块按图2所示重新拼合,这样就得到了一个13cm×5cm的长方形,面积是65cm2,面积多了1cm2,这是为什么?
小明给出如下证明:如图2,可知,tan∠CEF=![]() ,tan∠EAB=
,tan∠EAB=![]() ,∵tan∠CEF>tan∠EAB,∴∠CEF>∠EAB,∵EF∥AB,∴∠EAB+∠AEF=180°,∴CEF+∠AEF>180°,因此A、E、C三点不共线.同理A、G、C三点不共线,所以拼合的长方形内部有空隙,故面积多了1cm2
,∵tan∠CEF>tan∠EAB,∴∠CEF>∠EAB,∵EF∥AB,∴∠EAB+∠AEF=180°,∴CEF+∠AEF>180°,因此A、E、C三点不共线.同理A、G、C三点不共线,所以拼合的长方形内部有空隙,故面积多了1cm2
(1)小红给出的证明思路为:以B为原点,BC所在的直线为x轴,建立平面直角坐标系,证明三点不共线.请你帮小红完成她的证明;
(2)将13cmx13cm的正方形按上述方法剪开拼合,是否可以拼合成一个长方形,但面积少了1cm2?如果能,求出剪开的三角形的短边长;如果不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为支持国货,郑州格东律师事务所准备购买若干台华为电脑和华为手机奖励优秀员工.如果购买1台电脑,2部手机,一共需要花费10200元;如果购买2台电脑,1部手机一共需要花费13200元.
(1)求每台华为电脑和每部华为手机的价格分别是多少元?
(2)财务张经理交代会记小李,购买华为电脑和手机一共50台/部,并且手机部数不少于电脑台数的4倍,那么小李最多应准备多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰直角三角板的一个锐角顶点与正方形ABCD的顶点A重合,两边分别交BC、CD于M、N.
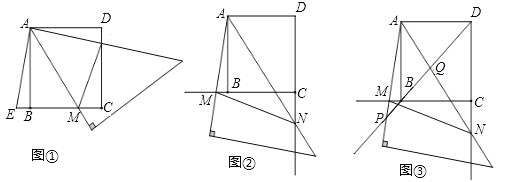
(1)如图①,作AE⊥AN交CB的延长线于E,求证:△ABE≌△AND;
(2)如图②,若M、N分别在边CB、DC所在的直线上时.
①求证:BM+MN=DN;②如图③,作直线BD交直线AM、AN于P、Q两点,若MN=10,CM=8,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,![]() 是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连结CE,DF,下列说法不正确的是
是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连结CE,DF,下列说法不正确的是![]()
![]()

A. 四边形CEDF是平行四边形
B. 当![]() 时,四边形CEDF是矩形
时,四边形CEDF是矩形
C. 当![]() 时,四边形CEDF是菱形
时,四边形CEDF是菱形
D. 当![]() 时,四边形CEDF是菱形
时,四边形CEDF是菱形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com