
【题目】如图,在△ABC和△DCB中,AB = DC,AC = DB,AC与DB交于点M.

【1】求证:△ABC≌△DCB
【2】过点C作CN∥BD,过点B作BN∥AC,CN与BN交于点N,试判断线段BN与CN的数量关系,并证明你的结论.
科目:初中数学 来源: 题型:
【题目】随着生活水平的提高,人们对饮水品质的需求越来越高,某市某公司根据市场需求代理A,B两种型号的净水器,每台A型净水器比每台B型净水器进价多200元,用5万元购进A型净水器与用4.5万元购进B型净水器的数量相等,
(1)求每台A型、B型净水器的进价各是多少元?
(2)该公司计划购进A,B两种型号的净水器共55台进行试销,其中A型净水器为m台,购买两种净水器的总资金不超过10.8万元.试销时A型净水器每台售价2500元,B型净水器每台售价2180元,该公司决定从销售A型净水器的利润中按每台捐献a(70<a<80)元作为公司帮扶贫困村饮水改造资金,设该公司售完55台净水器并捐献扶贫资金后获得的利润为W元,求W的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,将某四边形纸片ABCD的AB沿BC方向折过去(其中AB<BC),使得点A落在BC上,展开后出现折线BD,如图②.将点B折向D,使得B,D两点重叠,如图③,展开后出现折线CE,如图④.根据图④,下列关系正确的是( )
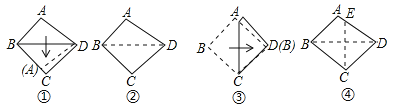
A. AD∥BCB. AB∥CDC. ∠ADB=∠BDCD. ∠ADB>∠BDC
查看答案和解析>>
科目:初中数学 来源: 题型:
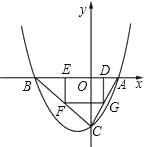
【题目】如图,已知抛物线P:y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F、G分别在线段BC、AC上,抛物线P上部分点的横坐标对应的纵坐标如下:
x | … | ﹣3 | ﹣2 | 1 | 2 | … |
y | … |
| ﹣4 |
| 0 | … |
(1)求A、B、C三点的坐标;
(2)若点D的坐标为(m,0),矩形DEFG的面积为S,求S与m的函数关系,并指出m的取值范围;
(3)当矩形DEFG的面积S取最大值时,连接DF并延长至点M,使FM=kDF,若点M不在抛物线P上,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,反比例函数![]() (k>0)图象经过等边△OAB的一个顶点B,点A坐标为(2,0),过点B作BM⊥x轴,垂足为M.
(k>0)图象经过等边△OAB的一个顶点B,点A坐标为(2,0),过点B作BM⊥x轴,垂足为M.
(1)求点B的坐标和k的值;
(2)若将△ABM沿直线AB翻折,得到△ABM',判断该反比例函数图象是从点M'的上方经过,还是从点M'的下方经过,又或是恰好经过点M',并说明理由;
(3)如图2,在x轴上取一点A1,以AA1为边长作等边△AA1B1,恰好使点B1落在该反比例函数图象上,连接BB1,求△ABB1的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A是以MN为直径的半圆上一个三等分点,点B是弧![]() 的中点,点P是半径ON上的点.若⊙O的半径为l,则AP+BP的最小值为( )
的中点,点P是半径ON上的点.若⊙O的半径为l,则AP+BP的最小值为( )
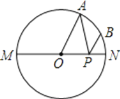
A. 2B. ![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
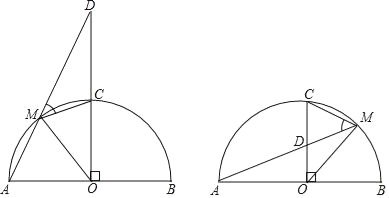
【题目】如图,AB是以O为圆心的半圆的直径,半径CO⊥AO,点M是![]() 上的动点,且不与点A、C、B重合,直线AM交直线OC于点D,连结OM与CM.
上的动点,且不与点A、C、B重合,直线AM交直线OC于点D,连结OM与CM.
(1)若半圆的半径为10.
①当∠AOM=60°时,求DM的长;
②当AM=12时,求DM的长.
(2)探究:在点M运动的过程中,∠DMC的大小是否为定值?若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尺规作图特有的魅力使无数人沉湎其中.传说拿破仑曾通过下列尺规作图将圆等分:
①将半径为r的⊙O六等分,依次得到A,B,C,D,E,F六个分点;
②分别以点A,D为圆心,AC长为半径画弧,两弧相交于点G;
③连接OG,以OG长为半径,从点A开始,在圆周上依次截取,刚好将圆等分.顺次连接这些等分点构成的多边形面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县教育局为了丰富初中学生的大课间活动,要求各学校开展形式多样的阳光体育活动.某中学就“学生体育活动兴趣爱好”的问题,随机调查了本校某班的学生,并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图:
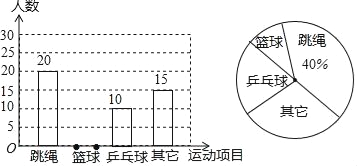
(1)在这次调查中,喜欢篮球项目的同学有 人,在扇形统计图中,“乒乓球”的百分比为 %,如果学校有800名学生,估计全校学生中有 人喜欢篮球项目.
(2)请将条形统计图补充完整.
(3)在被调查的学生中,喜欢篮球的有2名女同学,其余为男同学.现要从中随机抽取2名同学代表班级参加校篮球队,请直接写出所抽取的2名同学恰好是1名女同学和1名男同学的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com