
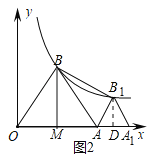
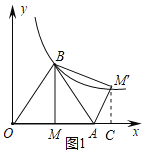
����Ŀ����ͼ1������������![]() (k>0)ͼ���ȱߡ�OAB��һ������B����A����Ϊ��2��0��������B��BM��x�ᣬ����ΪM��
(k>0)ͼ���ȱߡ�OAB��һ������B����A����Ϊ��2��0��������B��BM��x�ᣬ����ΪM��
��1�����B�������k��ֵ��
��2��������ABM��ֱ��AB���ۣ��õ���ABM'���жϸ÷���������ͼ���Ǵӵ�M'���Ϸ����������Ǵӵ�M'���·��������ֻ���ǡ�þ�����M'����˵�����ɣ�
��3����ͼ2����x����ȡһ��A1����AA1Ϊ�߳����ȱߡ�AA1B1��ǡ��ʹ��B1���ڸ÷���������ͼ���ϣ�����BB1�����ABB1�������

���𰸡���1��k��![]() ����2���÷���������ͼ���Ǵӵ�M'���·����������ɼ���������3����ABB1�����Ϊ
����2���÷���������ͼ���Ǵӵ�M'���·����������ɼ���������3����ABB1�����Ϊ![]() .
.
��������
��1������OABΪ�ȱ������μ�OA��2���ɵó�OM��BM�ij��������ɵó���B�����꣬�ɵ�B���������÷���������ͼ���ϵ���������������k��ֵ��
��2������M����M��C��x�ᣬ����Ϊ��C�����۵������ʣ���֪��AM����AM��1����BAM������BAM��60������Rt��ACM���У�ͨ����ֱ�������ο����AC��CM���ij��������ɵó�OC�ij������÷���������ͼ���ϵ�������������������������ͼ����ֱ��CM������������꣬�������M����������ȽϺɵó����ۣ�
��3������B1��B1D��x�ᣬ����Ϊ��D����AA1��a����AD��![]() a��B1D��
a��B1D��![]() a��OD��2��
a��OD��2��![]() a�������ɵó���B1�����꣬���÷���������ͼ���ϵ���������������a��ֵ�������ɵó�MD��B1D��AD�ij����ٽ��S��ABB1��S����BMDB1S��BMAS��ADB1���������ABB1�������
a�������ɵó���B1�����꣬���÷���������ͼ���ϵ���������������a��ֵ�������ɵó�MD��B1D��AD�ij����ٽ��S��ABB1��S����BMDB1S��BMAS��ADB1���������ABB1�������
��1���ߡ�OABΪ�ȱ������Σ�OA��2��
��OM��![]() OA��1��BM��
OA��1��BM��![]() OA��
OA��![]() ��
��
���B��������1��![]() ����
����
�߷���������![]() ͼ����B��
ͼ����B��
��k��![]() ��
��
��2���÷���������ͼ���Ǵӵ�M'���·��������������£�
����M����M��C��x�ᣬ����Ϊ��C����ͼ1��ʾ��
���۵������ʣ���֪��AM����AM��1����BAM������BAM��60����
���M��AC��180������BAM����BAM����60����
��Rt��ACM����AM����1����ACM����90������M��AC��60����
���AM��C��30����
��AC��![]() AM����
AM����![]() ��CM����
��CM����![]() AM����
AM����![]() ��
��
��OC��OA+AC��![]() ��
��
���M����������![]() ��
��![]() ����
����
��x��![]() ʱ��
ʱ��![]() ��
��
��![]() ��
��![]() ��
��
��÷���������ͼ���Ǵӵ�M'���·�������
��3������B1��B1D��x�ᣬ����Ϊ��D����ͼ2��ʾ��
��AA1��a����AD��![]() a��B1D��
a��B1D��![]() a��OD��2+
a��OD��2+![]() a��
a��
���B1��������2+![]() a��
a��![]() a����
a����
�ߵ�B1�ڸ÷���������![]() ��ͼ���ϣ�
��ͼ���ϣ�
�ࣨ2+![]() a��
a��![]() a��
a��![]() ��
��
��ã�a1����2![]() ��2����ȥ����a2��2
��2����ȥ����a2��2![]() ��2��
��2��
��MD��AM+AD��![]() ��B1D��
��B1D��![]() a��
a��![]() ��
��![]() ��AD��
��AD��![]() a��
a��![]() ��1��
��1��
��S��ABB1��S����BMDB1S��BMAS��ADB1
��![]() ��BM+B1D��MD��
��BM+B1D��MD��![]() BMAM��
BMAM��![]() B1DAD��
B1DAD��
![]() ��
��
![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=x2-2x-1��y���ڵ�A������A��AB��x�ύ�������ڵ�B����P���������ϣ�����PA��PB������P����x��ĶԳƵ�ǡ������ֱ��AB�ϣ����ABP�������______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����һ��ÿ���۸�Ϊ90Ԫ������Ʒ�����̳�����ʱ���֣����۵���![]() Ԫ
Ԫ![]() ��
��![]() ��ÿ��������
��ÿ��������![]() ��
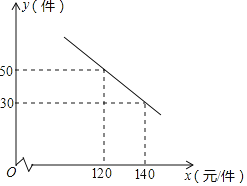
��![]() ֮��������ͼ��ʾ�Ĺ�ϵ��
֮��������ͼ��ʾ�Ĺ�ϵ��
![]() ���y��x֮��ĺ�����ϵʽ��
���y��x֮��ĺ�����ϵʽ��
![]() д��ÿ�������W�����۵���x֮��ĺ�����ϵʽ��������ۼ۶�Ϊ����ʱ��ÿ���õ����������������Ƕ��٣�
д��ÿ�������W�����۵���x֮��ĺ�����ϵʽ��������ۼ۶�Ϊ����ʱ��ÿ���õ����������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������![]() ��һ�κ���y��kx��1��ͼ������P��m����3m����
��һ�κ���y��kx��1��ͼ������P��m����3m����
��1�����P����������һ�κ����Ľ���ʽ��
��2������M��a��y1���͵�N��a+1��y2���������һ�κ�����ͼ���ϣ���ͨ�����������һ�κ��������ʣ�˵��y1����y2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ѧ���ϣ��ס��ҡ���������λͬѧ��ͬ�о����κ���y��x2��2x+c��c�dz����������֣��ú�����ͼ����x���һ�������ǣ���2��0�����ҷ��֣��ú�����ͼ����y��Ľ����ڣ�0����4���Ϸ��������֣�����xȡ�κ�ֵ���õ���yֵ��������c��y��1�������֣�����1��x��0ʱ���ú�����ͼ����x����·�����3��x��4ʱ���ú�����ͼ����x����Ϸ���ͨ����ʦ��������е�֪����λͬѧ��ֻ��һλͬѧ���ֵĽ����Ǵ���ģ����ͬѧ�ǣ�������
A. ��B. ��C. ��D. ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC����DCB�У�AB = DC��AC = DB��AC��DB���ڵ�M��

��1����֤����ABC�ա�DCB
��2������C��CN��BD������B��BN��AC��CN��BN���ڵ�N�����ж��߶�BN��CN��������ϵ����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
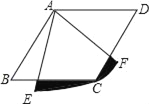
����Ŀ����ͼ���ı���ABCD�����Σ���B��60�㣬AB��1������AEF�İ뾶Ϊ1��Բ�Ľ�Ϊ60������ͼ����Ӱ���ֵ������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
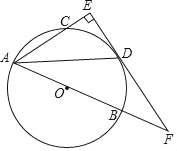
����Ŀ����ͼ��ABΪ��O��ֱ����CΪ��O��һ�㣬��CAB��ƽ���߽���O�ڵ�D������D��ED��AE������ΪE����AB���ӳ�����F��
��1����֤��ED�ǡ�O�����ߣ�
��2����AD��4![]() ��AB��6����FD�ij���
��AB��6����FD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABCD������AB��BC�ij��ǹ���x��һԪ���η��̷���![]() ������ʵ������
������ʵ������
��1����˵��������mȡ��ֵ��ԭ������������ʵ������
��2����mΪ��ֵʱ����ABCD�����Σ������ʱ���εı߳���
��3����AB��2����BC�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com