
【题目】已知反比例函数![]() 和一次函数y=kx﹣1的图象都经过点P(m,﹣3m).
和一次函数y=kx﹣1的图象都经过点P(m,﹣3m).
(1)求点P的坐标和这个一次函数的解析式;
(2)若点M(a,y1)和点N(a+1,y2)都在这个一次函数的图象上.试通过计算或利用一次函数的性质,说明y1大于y2.
【答案】(1)P的坐标(1,﹣3),y=﹣2x﹣1;(2)见解析.
【解析】
解:(1)将点P(m,3m)代入反比例函数解析式可得m=1;故P的坐标(1,3);再将点P(1,3)代入一次函数解析式可得:3=k1;故k=2;故一次函数的解析式为y=2x1;
(2)将M、N的值代入一次函数解析式可得y1=2a1,y2=2(a+1)1=2a3,做差可得y1y2=2a1(2a3),由a的值判断可得y1大于y2.
解:(1)将点P(m,﹣3m)代入反比例函数解析式可得:﹣3m=﹣3;即m=1,故P的坐标(1,﹣3),
将点P(1,﹣3)代入一次函数解析式可得:﹣3=k﹣1,故k=﹣2,
故一次函数的解析式为y=﹣2x﹣1;
(2)∵M、N都在y=﹣2x﹣1上,
∴y1=﹣2a﹣1,y2=﹣2(a+1)﹣1=﹣2a﹣3,
∴y1﹣y2=﹣2a﹣1﹣(﹣2a﹣3)=﹣1+3=2>0,
∴y1>y2.


科目:初中数学 来源: 题型:
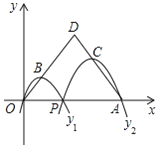
【题目】如图,已知点A(4,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=3时,这两个二次函数的最大值之和等于( )
A.![]() B.
B.![]() C.3 D.4
C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
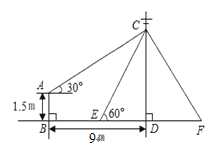
【题目】如图,在电线杆CD上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆9m的B处安置高为1.5m的测角仪AB,在A处测得电线杆上C处的仰角为30°,求拉线CE的长.(结果保留根号)
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,将某四边形纸片ABCD的AB沿BC方向折过去(其中AB<BC),使得点A落在BC上,展开后出现折线BD,如图②.将点B折向D,使得B,D两点重叠,如图③,展开后出现折线CE,如图④.根据图④,下列关系正确的是( )
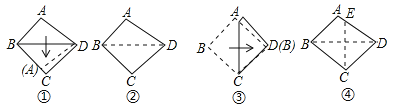
A. AD∥BCB. AB∥CDC. ∠ADB=∠BDCD. ∠ADB>∠BDC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家快递公司揽件员(揽收快件的员工)的日工资方案如下:
甲公司为“基本工资+揽件提成”,其中基本工资为70元/日,每揽收一件提成2元;
乙公司无基本工资,仅以揽件提成计算工资.若当日揽件数不超过40,每件提成4元;若当日搅件数超过40,超过部分每件多提成2元.
如图是今年四月份甲公司揽件员人均揽件数和乙公司搅件员人均揽件数的条形统计图:

(1)现从今年四月份的30天中随机抽取1天,求这一天甲公司揽件员人均揽件数超过40(不含40)的概率;
(2)根据以上信息,以今年四月份的数据为依据,并将各公司揽件员的人均揽件数视为该公司各揽件员的
揽件数,解决以下问题:
①估计甲公司各揽件员的日平均件数;
②小明拟到甲、乙两家公司中的一家应聘揽件员,如果仅从工资收入的角度考虑,请利用所学的统计知识帮他选择,井说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
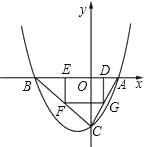
【题目】如图,已知抛物线P:y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F、G分别在线段BC、AC上,抛物线P上部分点的横坐标对应的纵坐标如下:
x | … | ﹣3 | ﹣2 | 1 | 2 | … |
y | … |
| ﹣4 |
| 0 | … |
(1)求A、B、C三点的坐标;
(2)若点D的坐标为(m,0),矩形DEFG的面积为S,求S与m的函数关系,并指出m的取值范围;
(3)当矩形DEFG的面积S取最大值时,连接DF并延长至点M,使FM=kDF,若点M不在抛物线P上,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,反比例函数![]() (k>0)图象经过等边△OAB的一个顶点B,点A坐标为(2,0),过点B作BM⊥x轴,垂足为M.
(k>0)图象经过等边△OAB的一个顶点B,点A坐标为(2,0),过点B作BM⊥x轴,垂足为M.
(1)求点B的坐标和k的值;
(2)若将△ABM沿直线AB翻折,得到△ABM',判断该反比例函数图象是从点M'的上方经过,还是从点M'的下方经过,又或是恰好经过点M',并说明理由;
(3)如图2,在x轴上取一点A1,以AA1为边长作等边△AA1B1,恰好使点B1落在该反比例函数图象上,连接BB1,求△ABB1的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
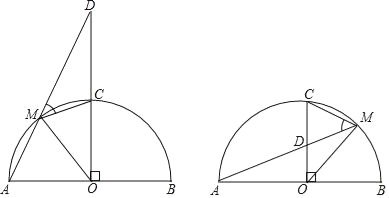
【题目】如图,AB是以O为圆心的半圆的直径,半径CO⊥AO,点M是![]() 上的动点,且不与点A、C、B重合,直线AM交直线OC于点D,连结OM与CM.
上的动点,且不与点A、C、B重合,直线AM交直线OC于点D,连结OM与CM.
(1)若半圆的半径为10.
①当∠AOM=60°时,求DM的长;
②当AM=12时,求DM的长.
(2)探究:在点M运动的过程中,∠DMC的大小是否为定值?若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
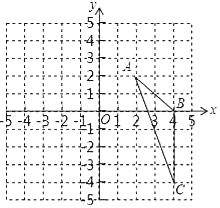
【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4).
(1)请在图中,画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)以点O为位似中心,将△ABC缩小为原来的![]() ,得到△A2B2C2,请在图中y轴右侧,画出△A2B2C2,并求出∠A2C2B2的正弦值.
,得到△A2B2C2,请在图中y轴右侧,画出△A2B2C2,并求出∠A2C2B2的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com