
【题目】如图①,将某四边形纸片ABCD的AB沿BC方向折过去(其中AB<BC),使得点A落在BC上,展开后出现折线BD,如图②.将点B折向D,使得B,D两点重叠,如图③,展开后出现折线CE,如图④.根据图④,下列关系正确的是( )
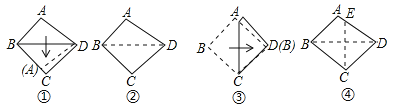
A. AD∥BCB. AB∥CDC. ∠ADB=∠BDCD. ∠ADB>∠BDC
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克 40 元,规定每千克售价不低于成本,且不高于 80 元,经市场调查,每天的销售量 y( 千克)与每千克售价x(元)满足一次函数关系,部分数据如表:

(1)求 y 与 x 之间的函数表达式;
(2)设商品每天的总利润为 W(元),求 W 与 x 之间的函数表达式(利润=收入﹣成本);
(3)指出售价为多少元时获得利润最大?并试说明(2)中总利润W随售价x的变化而变化的情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,∠B=60°,AB=2cm,E、F分别是BC、CD的中点,连接AE、EF、AF,则△AEF的周长为( )

A. 2![]() cm B. 3
cm B. 3![]() cm C. 4
cm C. 4![]() cm D. 3cm
cm D. 3cm
查看答案和解析>>
科目:初中数学 来源: 题型:
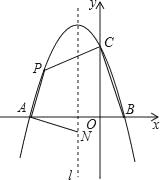
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为x=﹣1.
(1)求抛物线的解析式并写出其顶点坐标;
(2)若动点P在第二象限内的抛物线上,动点N在对称轴l上.
①当PA⊥NA,且PA=NA时,求此时点P的坐标;
②当四边形PABC的面积最大时,求四边形PABC面积的最大值及此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一种每件价格为90元的新商品,在商场试销时发现:销售单价![]() 元
元![]() 件
件![]() 与每天销售量
与每天销售量![]() 件
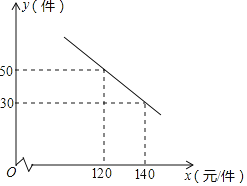
件![]() 之间满足如图所示的关系.
之间满足如图所示的关系.
![]() 求出y与x之间的函数关系式;
求出y与x之间的函数关系式;
![]() 写出每天的利润W与销售单价x之间的函数关系式,并求出售价定为多少时,每天获得的利润最大?最大利润是多少?
写出每天的利润W与销售单价x之间的函数关系式,并求出售价定为多少时,每天获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在三角形ABC中,AB=6,AC=BC=5,以BC为直径作⊙O交AB于点D,交AC于点G,直线DF是⊙O的切线,D为切点,交CB的延长线于点E.
(1)求证:DF⊥AC;
(2)求tan∠E的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 和一次函数y=kx﹣1的图象都经过点P(m,﹣3m).
和一次函数y=kx﹣1的图象都经过点P(m,﹣3m).
(1)求点P的坐标和这个一次函数的解析式;
(2)若点M(a,y1)和点N(a+1,y2)都在这个一次函数的图象上.试通过计算或利用一次函数的性质,说明y1大于y2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DCB中,AB = DC,AC = DB,AC与DB交于点M.

【1】求证:△ABC≌△DCB
【2】过点C作CN∥BD,过点B作BN∥AC,CN与BN交于点N,试判断线段BN与CN的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为支持国货,郑州格东律师事务所准备购买若干台华为电脑和华为手机奖励优秀员工.如果购买1台电脑,2部手机,一共需要花费10200元;如果购买2台电脑,1部手机一共需要花费13200元.
(1)求每台华为电脑和每部华为手机的价格分别是多少元?
(2)财务张经理交代会记小李,购买华为电脑和手机一共50台/部,并且手机部数不少于电脑台数的4倍,那么小李最多应准备多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com