
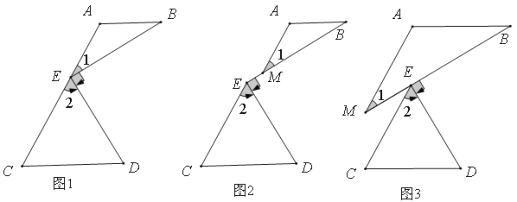
【题目】(1)已知:如图1,BE⊥DE,∠1=∠B,∠2=∠D,试证明AB与CD平行。
(2)若图形变化为如图2、图3所示,且满足AB∥ CD,BE⊥DE,∠1=∠B,∠2=∠D,那么∠1与∠2有怎样的关系?选择一个图形进行证明。
【答案】(1)证明见解析;(2)∠1+∠2=90°;证明见解析.
【解析】试题分析:(1)过点E作EN∥AB,根据平行线的性质得到∠BEN=∠B,等量代换得到∠BEN=∠1,推出∠D=∠DEN,根据平行线的判定即可得到结论;
(2)如答图2,过点E作EN∥AB,根据平行线的性质得到∠B=∠1,量代换得到∠BEN=∠1,推出EN∥CD,于是得到结论.
试题解析:
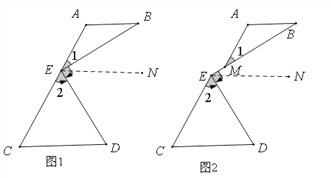
(1)过点E作EN∥AB,
则∠BEN=∠B,∵∠1=∠B,
∴∠BEN=∠1,
∵∠BEN+∠DEN=∠BED=90,
∴∠1+∠2=90,
∴∠2=∠DEN,
∵∠2=∠D,
∴∠D=∠DEN,
∴AB∥CD;
(2)
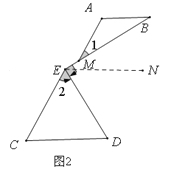
如答图2,过点E作EN∥AB,
∴∠BEN=∠B,
∵∠B=∠1,
∴∠BEN=∠1,
∵∠BED=90=∠BEN+∠DEN,∠1+∠2=90,
∴∠DEN=∠2,
∵∠2=∠D,
∴EN∥CD,
∴AB∥CD.


科目:初中数学 来源: 题型:
【题目】用配方法解一元二次方程x2﹣6x=8时,此方程可变形为( )
A.(x﹣3)2=17
B.(x﹣3)2=1
C.(x+3)2=17
D.(x+3)2=1
查看答案和解析>>
科目:初中数学 来源: 题型:
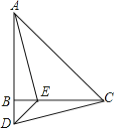
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC.
①求证:△ABE≌△CBD;
②若∠CAE=30°,求∠BDC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
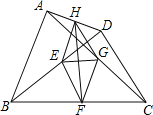
【题目】如图,E、F、G、H分别是BD、BC、AC、AD的中点,且AB=CD.下列结论:①EG⊥FH,②四边形EFGH是矩形,③HF平分∠EHG,④EG=![]() (BC-AD),⑤四边形EFGH是菱形.其中正确的个数是 ( )
(BC-AD),⑤四边形EFGH是菱形.其中正确的个数是 ( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设先发车辆行驶的时间为x h,两车之间的距离为y km,图中的折线表示y与x之间的函数关系.根据图象解决以下问题:
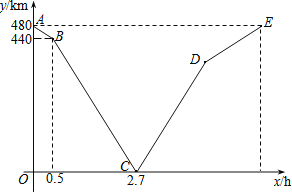
(1)慢车的速度为 km/h,快车的速度为 km/h;
(2)解释图中点D的实际意义并求出点D的坐标;
(3)求当x为多少时,两车之间的距离为300km.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系中,△ABC的位置如图所示.
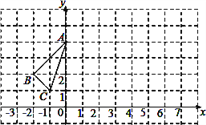
(1)请写出A、B、C三点的坐标;
(2)请求出△ABC的面积;
(3)将△ABC向右平移6个单位,再向上平移2个单位,请在图中作出平移后的△A′B′C′.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com